LLM 学习笔记2-神经网络
神经网络基础,RNN,CNN,Seq2Seq,Transformer
简单神经网络
机器学习。
神经网络:模仿人脑结构设计出来的一种架构,最小的学习单元是 神经元。
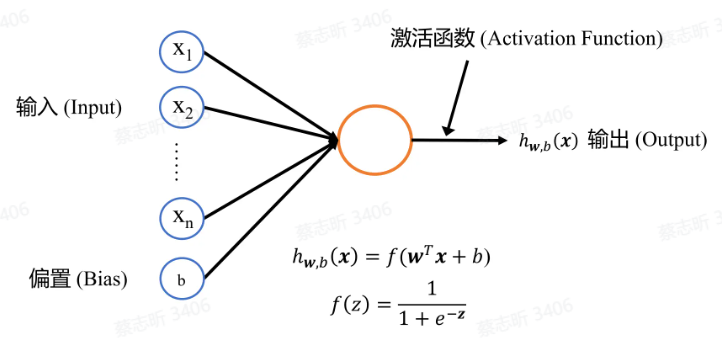
神经元是一个 计算单元,由 n 维输入 $x$,偏置 $n$,n 维权重 $w$,激活函数 $f(z)$ 构成,$w, b$ 是神经元的 参数。
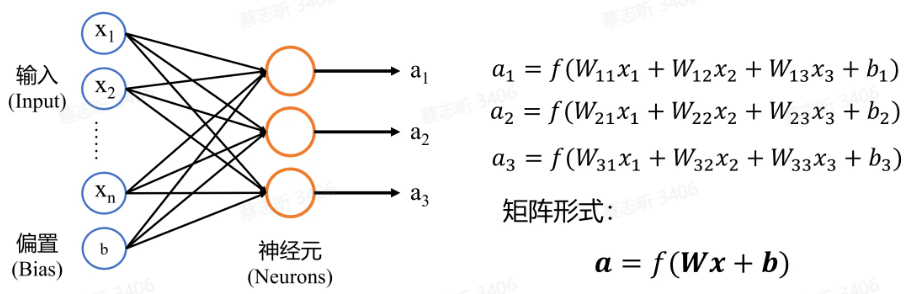
单层神经网络:由许多简单神经元连接在一起组成。
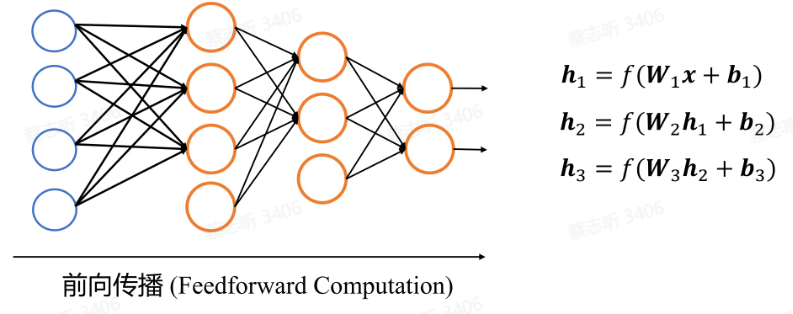
多层神经网络:由多个单层神经网络堆叠而成,中间输出被称为隐藏状态。
为什么要有激活函数
如果没有激活函数,运算就会退化成简单的矩阵乘法,表达能力会更弱。同时保证层数增加时不会退化成单层的网络。
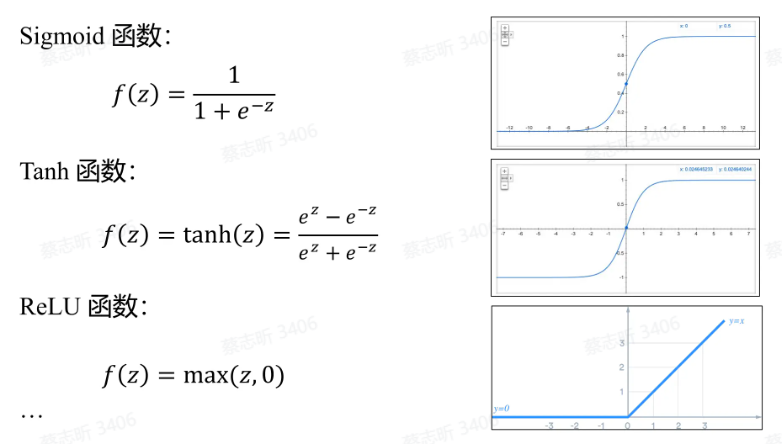
常见的激活函数:
为什么要让神经网络层数变多
单层神经网络表达能力有限,在中间层中可以提取出一些有用的信息。
如何训练神经网络
训练目标:在给定的训练样本上,通过优化模型参数,使得模型输出与实际值之间的差异最小化。
$(x_i, y_i) $ 为给定的训练样本, $ x_i $ 是输入, $ y_i $ 是对应的输出, $ i $ 表示样本的编号,共有 $ N $ 个训练样本。希望训练一个神经网络 $ F_\theta(\cdot) $,它将 $ x $ 作为输入,并预测 $ y $。其中 $ \theta $ 是神经网络 $ F_\theta(\cdot) $ 的参数。
训练目标是 最小化损失函数,数学表达式为: \(\min_{\theta} J(\theta) = \min_{\theta} \frac{1}{N} \sum_{i=1}^{N} l(y_i - F_\theta(x_i))\) 其中:
- $ J(\theta) $ 是需要最小化的总体损失函数。
- $ l(y_i - F_\theta(x_i)) $ 是单个样本损失函数,用来衡量神经网络预测输出 $ F_\theta(x_i) $ 与真实输出 $ y_i $ 之间的差异。
随机梯度下降法:通过对模型参数 $ \theta $ 进行迭代更新,使损失函数逐渐减小,从而找到损失函数的最小值。
更新公式为: \(\theta^{\text{new}} = \theta^{\text{old}} - \alpha \nabla_\theta J(\theta)\) 其中:
- $ \theta^{\text{new}} $ 表示新的模型参数。
- $ \theta^{\text{old}} $ 表示旧的模型参数。
- $ \alpha $ 是学习率,用来控制每次更新的步伐大小。
- $ \nabla_\theta J(\theta) $ 是损失函数 $ J(\theta) $ 对参数 $ \theta $ 的梯度,即导数。
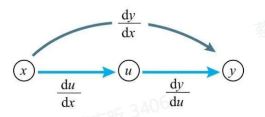
梯度:对于一个函数 $ F(x) $,假设函数有 $ N $ 个输入 $ x = (x_1, x_2, \ldots, x_N) $ 和一个输出 $ F(x) $,那么梯度是对每个输入 $ x_i $ 求偏导数所得到的向量,即: \(\nabla F(x) = \left[ \frac{\partial F}{\partial x_1}, \frac{\partial F}{\partial x_2}, \ldots, \frac{\partial F}{\partial x_N} \right]\) 反向传播(BP):反向传播是基于链式法则 计算梯度 的过程。它是一种在深度学习框架(如TensorFlow,PyTorch)中广泛使用的算法。
循环神经网络和卷积神经网络
语言建模:预测下一个词。
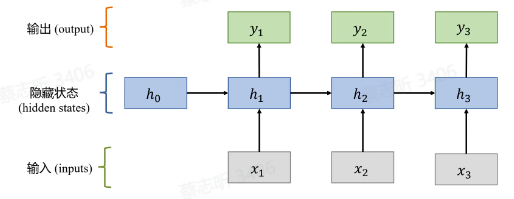
循环神经网络 RNN
关键:处理序列数据时的顺序记忆
主要思想:一种能够识别 序列模式 的机制
递归的更新序列记忆,对序列数据建模。
精髓:隐状态的计算。
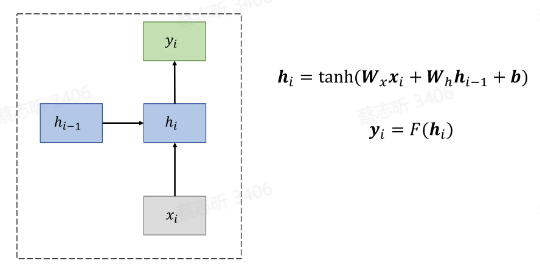
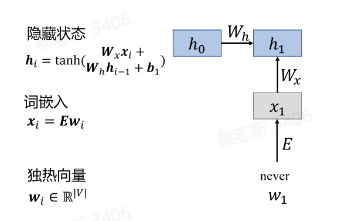
$ h_i = \tanh(W_x x_i + W_h h_{i-1} + b) $
- 这是 RNN 单元的隐藏状态更新公式。
- $ h_i $:当前时刻 $ i $ 的隐藏状态。
- $ W_x $:输入权重矩阵,决定当前输入 $ x_i $ 对隐藏状态的影响。
- $ W_h $:隐藏层的权重矩阵,决定上一时刻的隐藏状态 $ h_{i-1} $ 对当前隐藏状态的影响。
- $ b $:偏置项。
- $ \tanh $:非线性激活函数,常用来增加模型的表达能力,输出值范围在 $[-1, 1]$。
- $ x_i $:当前时刻的输入。
- $ h_{i-1} $:上一时刻的隐藏状态。
$ y_i = F(h_i) $
- $ F $:输出层的函数,可以是一个线性函数,也可以是其他激活函数(如 softmax、sigmoid 等),具体取决于任务类型(分类、回归等)。
RNN 的一个显著特点是它在计算当前输出 $ y_i $ 时,会综合考虑当前输入 $ x_i $ 和上一时刻的隐藏状态 $ h_{i-1} $,从而实现对序列信息的捕捉。
通过循环结构,RNN 可以处理序列数据,使得前一个时刻的信息传递给后一个时刻,适合处理时间序列、自然语言处理等任务。
一个例子:
独热向量:词库 $V$ 里有 $ V $ 个词,可以把每个词看作是一个 $ V $ 维向量中的一维,$1$ 就表是是这个词。因此每个词都可以表示为一个单位向量。 - 词嵌入:输入 RNN 之前进行 Embedding,矩阵降维。
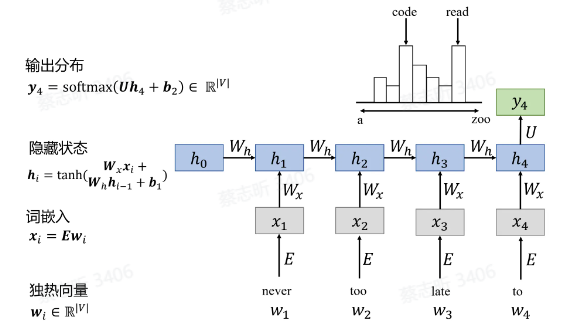
$h_4$ 里应当包含了前面所有输入的信息,$U$ 是连接隐藏层和输出层的权重矩阵,$b_2$ 是输出层的偏置。softmax 函数的作用是将网络的线性输出转化为 概率分布,表示模型认为每个词是下一个词的可能性。
$y_4$ 是一个概率分布,表示在输入句子的上下文中,模型预测下一个词的可能性。每个元素代表词表中对应单词作为下一个词的概率。
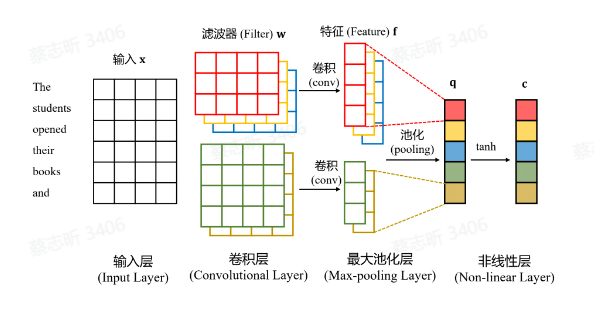
卷积神经网络 CNN
计算句子中所有 N-gram(表示对于给定序列,连续的 n 个词的子序列) 短语的表示(语言模型的一种退化,只关心最近的 n 个词对下一个词的影响)。
擅长提取局部和位置不变的模式。
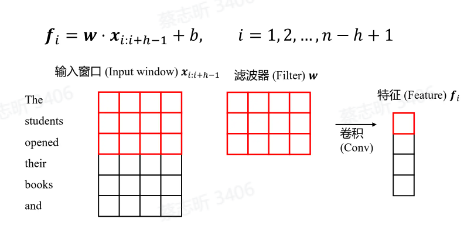
移动固定长度的窗口,依次得到特征。
| CNNs | RNNs | |
|---|---|---|
| 优点 | 提取局部和位置不变特征 | 建模长距离依赖关系 |
| 参数 | 参数更少 | 参数更多 |
| 并行化 | 在句子内能更好的并行处理 | 不能在句子内并行处理 |
Seq2Seq 和 Transformers
Seq2Seq:将一个序列转换成另一个序列的任务。
Seq2Seq 模型的主要部分:
- Encoder 编码器:接收输入序列,将其转换为一个固定大小的上下文向量(通常是隐状态表示)。
- Decoder 解码器:用编码器生成的上下文向量,将其解码为目标序列。
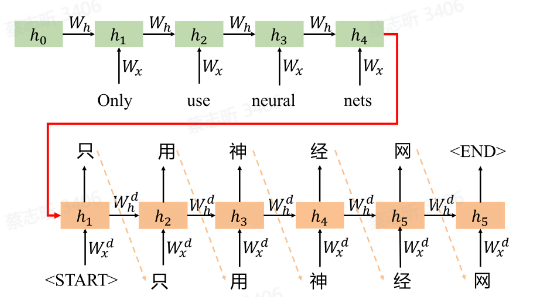
最早是用 RNN 做的:
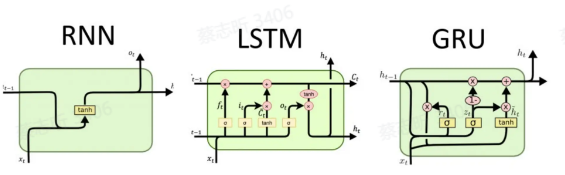
更好的 Seq2Seq 架构:Transformer
主要是把处理序列的 RNN 替换掉了。
引入了 注意力机制。(TODO: 读一下 Attention is all you need)
传统的 RNN 往后推导都是基于 Encoder 把 source 转换出来的中间编码做的,Decoder 推每一个词都是基于这个中间编码来推。但其实 source 里每一个词对于 decoder 中不同的词的影响是不一样的,采用注意力机制为 encoder 中不同的词分配不同的权重,加到输入里。