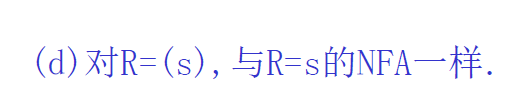2024秋编译原理理论复习

Posted Dec 11, 2024 Updated Feb 10, 2025

By Zhixin Cai

35 min read

2024秋编译原理理论复习

编译原理理论复习

大题考点：

NFA 确定化，DFA 最小化 √
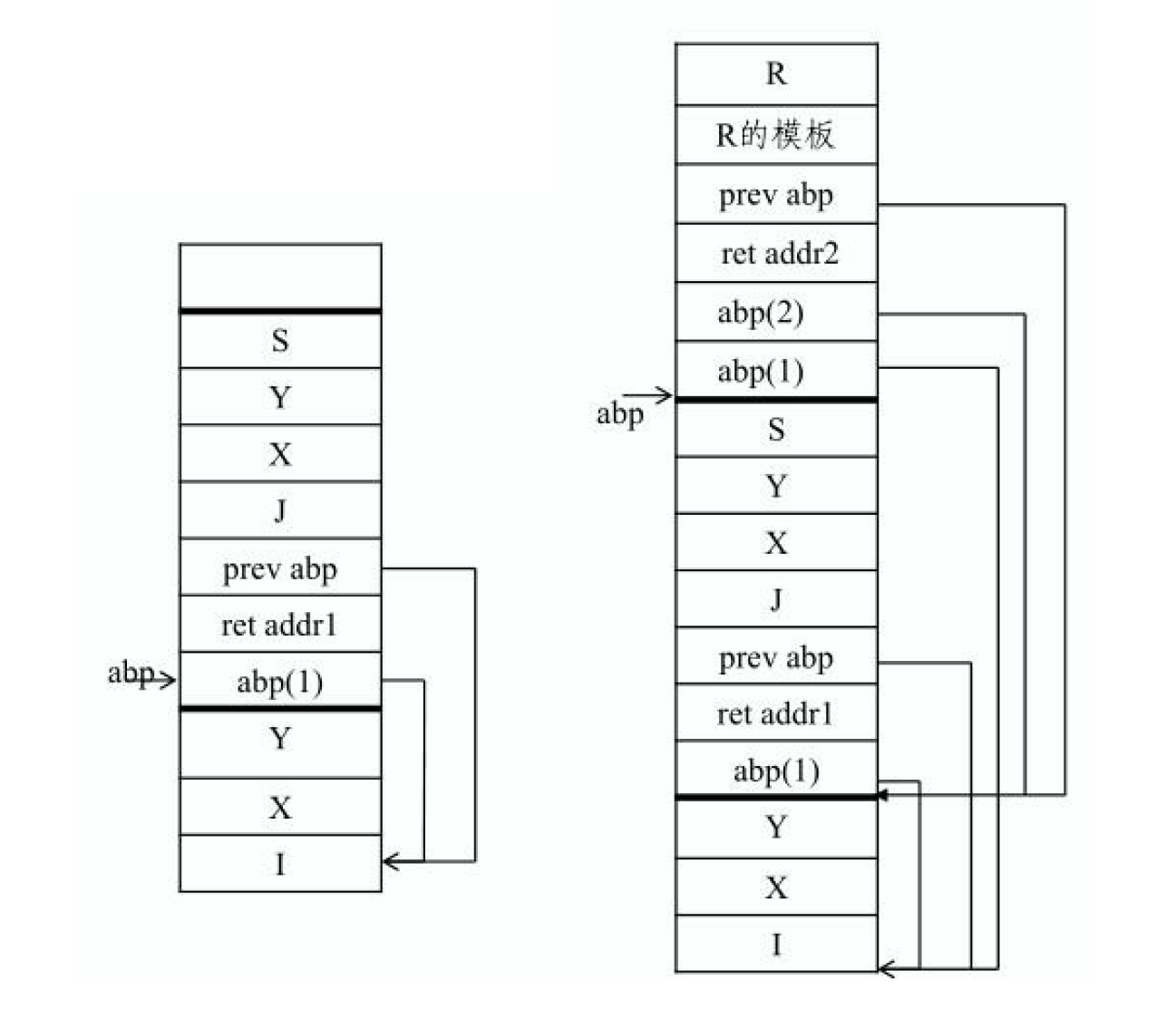
分析运行栈 √
求FIRST和FOLLOW，判断是否是LL（1）文法 √
求FIRSTVT和LASTVT，构造优先关系矩阵，判断是否是算符优先文法 √
拓广文法，求LR（0）项目集规范族，构造Action和Goto。√
代码优化：流图，DAG消基本块优化，活跃变量分析，画冲突图，图着色寄存器分配

复习时发现的问题：

素短语：至少包含一个终结符的短语，且不再包含其它素短语。
若 $\alpha \stackrel{*}{\Rightarrow} \varepsilon$，则规定 $\varepsilon \in \text{FIRST}(\alpha)$
~~算符优先文法的规约过程？每次规约最左素短语（怎么规约？）~~ 好像不考了
构建符号表，~~需要进行出栈操作吗？~~
运行栈怎么写？注意 运行时 的符号表，要找到程序的入口一点一点调用下去分析。
用一个例子来理解。
求活前缀的有效项目集：状态图沿着活前缀走一遍，走到的状态。（规约（r）可以理解为往回走？）
寄存器：通用寄存器（保留寄存器，临时寄存器，全局寄存器），专用寄存器

2 文法语言

规范推导：最右推导，先推右边的非终结符

语法树

短语：每个子树的根的符号串

简单短语：高度为2的子树的根符号串

句柄：最左简单短语

规约和推导互为逆过程，规范规约从句柄开始规约。

多余规则：不可达、不活动

3 词法分析

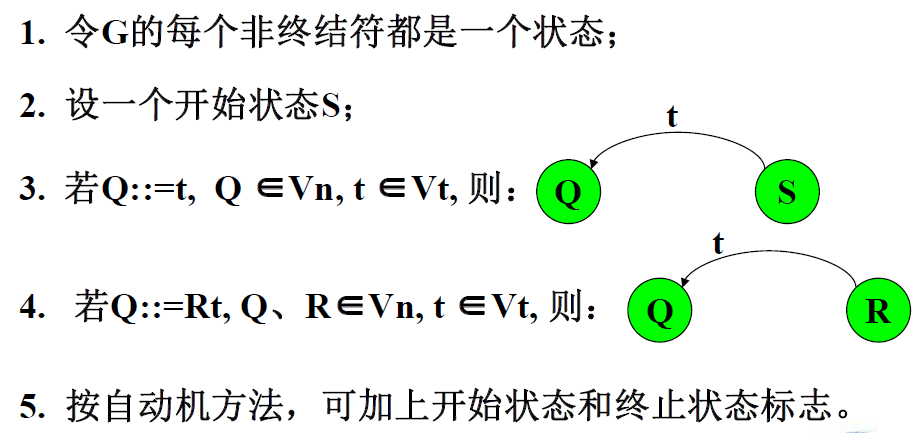
左线性文法的状态图画法

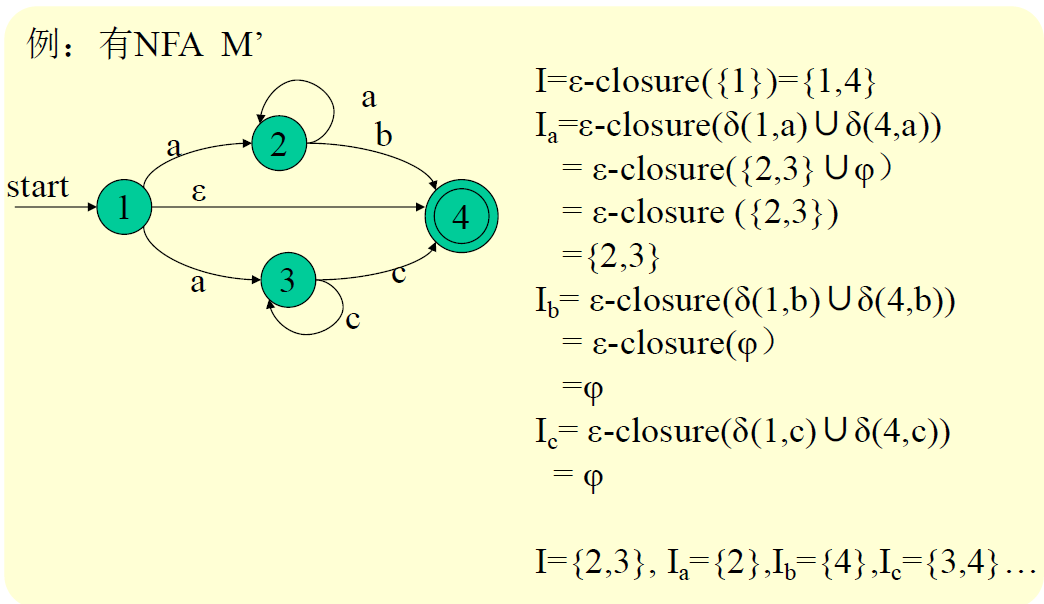
NFA 的确定化

定义1、集合I的ε-闭包：

令I是一个状态集的子集，定义ε-closure（I）为：

1）若s ∈ I，则s ∈ ε-closure（I）；

2）若s ∈ I，则从s出发经过任意条ε弧能够到达的任何状态都属于ε-closure（I）。

状态集ε-closure（I）称为I的ε-闭包。

定义2

令I是NFA M’的状态集的一个子集，a ∈ Σ

定义：I_a = ε-closure(J)

其中J = ∪ δ(s, a)

– J是从状态子集I中的每个状态出发，经过标记为a的弧而达到的状态集合。

– I_a是状态子集，其元素为J中的状态，加上从J中每一个状态出发通过ε弧到达的状态。

从start开始，求出走每条边可以到达的点集。然后再对求出的每个点集求走每条边可以到达的点集。最后把点集编号并形成状态转移矩阵。包含原初始状态的点集是初态，包含原终止状态的点集是终态。

DFA 最小化

一个有穷自动机可以通过 消除多余状态 和 合并等价状态 而转换成一个最小的与之等价的有穷自动机。

合并等价状态：分割法，把一个DFA(不含多余状态)的状态分割成一些不相关的子集，使得任何不同的两个子集状态都是可区别的，而同一个子集中的任何状态都是等价的。

过程：先区分终态与非终态，分成两个区，然后一点一点观察1，如果有几个点的转移结果都在同一个区，就可以把他们划分成一个区。详见第三章ppt第57页的例子。

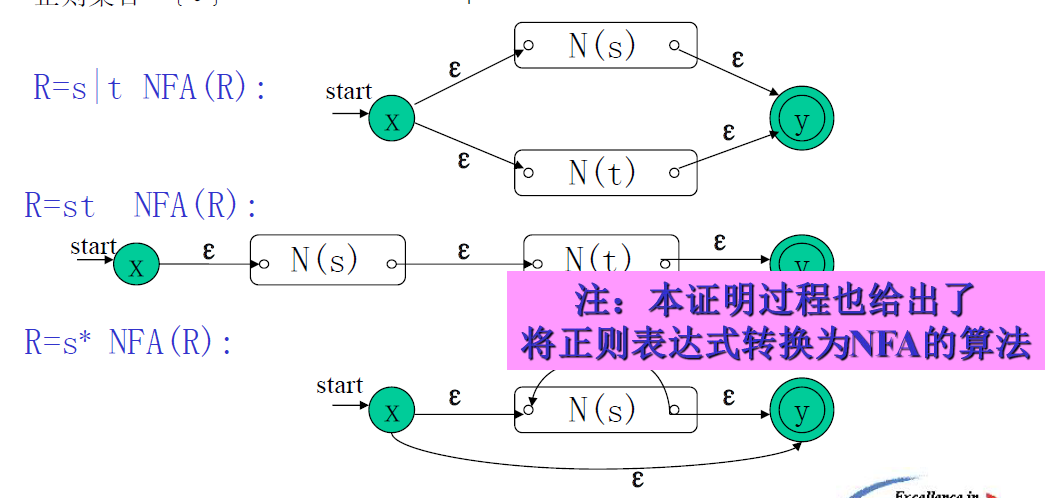
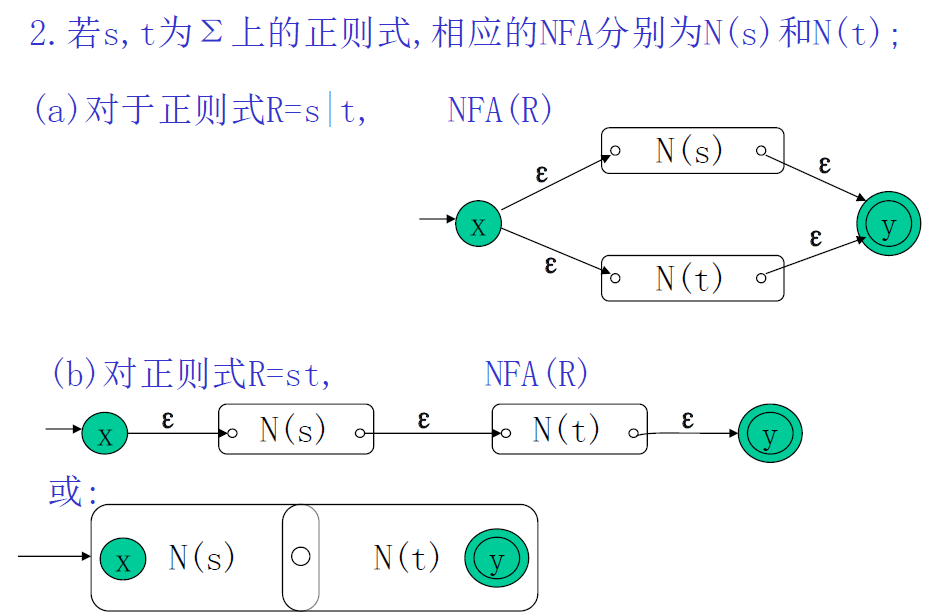
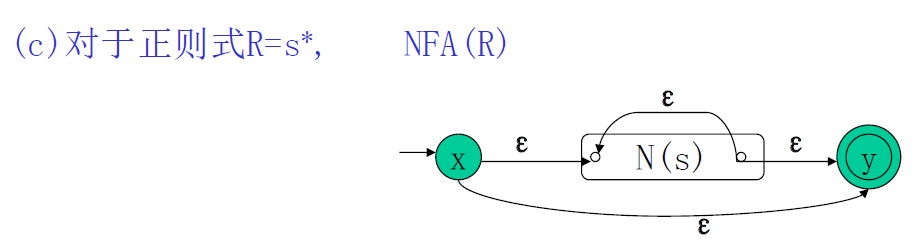
正则表达式转 NFA

N(s) 和 N(t) 代表的是非确定有限自动机（NFA）的状态转换图，它们分别对应正则表达式 ( s ) 和 ( t ) 的NFA表示。

LEX

详见书254页。

对每个识别规则构造 DFA，然后合并成一个NFA（用空边转到每个识别规则的start），再转成DFA。终态如果有二义性，遵照最长匹配原则和优先匹配原则。

分析一个字符串，分析到没有后继状态为止，然后退回去反序找终态。

有穷自动机→正则文法

正则文法→有穷自动机

正则表达式→有穷自动机

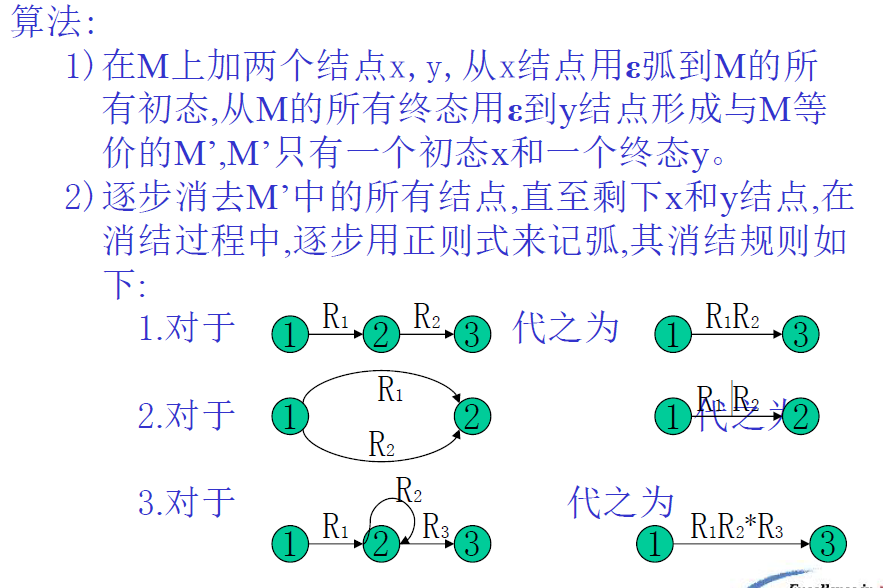
有穷自动机→正则表达式

正则文法→正则表达式

正则表达式→正则文法

4 语法分析

自顶而下分析

分析过程是设法建立一棵语法树,使语法树的末端结点与给定符号串相匹配。

问题

不能处理左递归文法
- 使用扩充的BNF表示来改写（PPT12页）
  规则一：（提因子）
  规则二：U:: =x y …… z Uv, 则U:: =(x y …… z){v}
- 改为右递归
  规则三：右递归P:: =Pα β，则P:: = β P’， P’:: = αP’ ε
- 一般方法（间接左递归）：一直代入，代到有左递归为止，然后消左递归
回溯
设文法G（不具左递归性），U ∈ Vn
U ::= α1 α2 α3
[定义] FIRST(αi) = {a αi *⇒ a…, a ∈ Vt}
为避免回溯，对文法的要求是：
FIRST(αi) ∩ FIRST(αj) = ∅ (i ≠ j)
- 改写文法，对具有多个右部的规则反复提取左因子
  例1 U:: =xV xW U, V, W ∈ Vn, x ∈ Vt+
  改写为 U:: =x(V W)
  更清楚地表示为: U:: =xZ Z:: =V W
- 超前扫描

LL 分析法

见书256页。关键是把分析表画出来，然后产生式是反序压入栈的（最左推导）。

构造分析表
- FIRST
  假定 $\alpha$ 是文法 $G$ 的任一符号串，或者说 $\alpha \in (V_t \cup V_n)^*$，定义：
  \[\text{FIRST}(\alpha) = \{ a \mid \alpha \stackrel{*}{\Rightarrow} a \cdots, a \in V_t \}\]
  特别是，若 $\alpha \stackrel{*}{\Rightarrow} \varepsilon$，则规定 $\varepsilon \in \text{FIRST}(\alpha)$，换句话说，$\text{FIRST}(\alpha)$ 是从 $\alpha$ 可能推导出的所有符号串的 第一个终结符号 或可能的 $\varepsilon$ 组成的集合。
  构造时注意对 $\varepsilon$ 的处理。
- FOLLOW
  假定 $S$ 是文法的开始符号，对于 $G$ 的任何非终结符 $A$，定义：
  $ FOLLOW(A) = { a \mid S \stackrel{*}{\Rightarrow} \cdots Aa \cdots, a \in V_t } $
  特别是，若 $S \stackrel{*}{\Rightarrow} \cdots A$，则规定 $# \in FOLLOW(A)$。换句话说，$FOLLOW(A)$ 是所有句型中出现在 紧接 $A$ 之后的终结符 或 $#$(表示输入结束)组成的集合。
  构造集合 $FOLLOW$ 的算法
  对于 $G[S]$ 中的每一个 $A \in V_n$，为构造相应的 $FOLLOW(A)$，可反复应用如下规则，直到每一个 $FOLLOW$ 集不再增大为止。
  （1）对于文法的开始符号 $S$，令 $#\in FOLLOW(S)$。
  （2）若 $G$ 中有形如 $A \rightarrow \alpha B \beta$ 的产生式，且 $\beta \neq \varepsilon$，则将 $FIRST(\beta)$ 中的一切非 $\varepsilon$ 符号加进 $FOLLOW(B)$ 中。
  （3）若 $G$ 中有形如或 $A \rightarrow \alpha B \beta$ 的产生式，且 $\varepsilon \in FIRST(\beta)$，则 $FOLLOW(A)$ 中的全部元素均属于 $FOLLOW(B)$。
- 构造分析表
  为构造 $G$ 的 LL(1) 分析表 $M$，则只需对 $G$ 中的每一产生式 $A \rightarrow \alpha$，依如下规则确定 $M$ 的各个元素：
  （1）对 $FIRST(\alpha)$ 中的每一终结符 $a$，置 $M[A, a]$ 为 “$A \rightarrow \alpha$”。
  （2）若 $\varepsilon \in FIRST(\alpha)$，则对属于 $FOLLOW(A)$ 的每一符号 $b$（$b$ 为终结符或 #），置 $M[A, b]$ 为 “$A \rightarrow \varepsilon$”。
  （3）把 $M$ 中所有不满足规则（1）、（2）定义的元素均置为空，即为 “error”，表示出错。
- 如果分析表不含多重定义元素，那就是 LL(1) 文法，一个 LL(1) 文法是无二义性的。
  可以证明，一个文法 $G$ 是 LL(1) 的，当且仅当对于 $G$ 的每一个非终结符 $A$ 的任何两条不同规则 $A ::= \alpha \mid \beta$，下面的条件成立：
  （1）$\text{FIRST}(\alpha) \cap \text{FIRST}(\beta) = \emptyset$，也就是由 $\alpha$ 和 $\beta$ 推导不出以某个同一终结符 $a$ 为首符号的符号串；它们也不应该都能推出空符号串 $\varepsilon$。
  （2）假若 $\beta \stackrel{}{\Rightarrow} \varepsilon$，那么 $\text{FIRST}(\alpha) \cap \text{FOLLOW}(A) = \emptyset$；也就是说，若 $\beta \stackrel{}{\Rightarrow} \varepsilon$，则 $\alpha$ 所能推出的符号串的首符号不应在 $\text{FOLLOW}(A)$ 中。

自底向上分析

把符号推到栈中并检查是否可以形成句柄后进行规约。

算符优先分析

仿效四则运算过程，预先规定相邻终结符之间的优先关系，然后利用这种优先关系来确定句型的“句柄” ，并进行归约。

分析过程：和四则运算很像，如果符号栈顶的符号优先级比将要进栈的符号高，那么就进行规约；优先级相等则弹出栈；否则进符号栈。详见书268页。

算符优先文法

算符文法（OG文法）：没有两个非终结符相邻
算符优先关系：
(1) $a = b$，当且仅当文法中有形如 $U ::= \cdots ab \cdots$ 或 $U ::= \cdots aVb \cdots$ 的规则。
(2) $a < b$，当且仅当文法中有形如 $U ::= \cdots aW \cdots$ 的规则，其中 $W \stackrel{+}{\Rightarrow} b \cdots$ 或 $W \stackrel{+}{\Rightarrow} Vb \cdots$。
(3) $a > b$，当且仅当文法中有形如 $U ::= \cdots Wb \cdots$ 的规则，其中 $W \stackrel{+}{\Rightarrow} \cdots a$ 或 $W \stackrel{+}{\Rightarrow} aV$。
总的来说就是，在非终结符里面的符号更大一些。
算符优先文法：任意两个终结符之间最多只有一种关系成立。

构建优先关系矩阵

$=$ 可以遍历找到。
FIRSTVT
$ \text{FIRSTVT}(U) = { b \mid U \stackrel{+}{\Rightarrow} b \cdots \text{或} U \stackrel{+}\Rightarrow Vb \cdots, b \in V_t, \text{而} V \in V_n } $
FIRST，以及在开头非终结符后面的终结符
LASTVT
$ \text{LASTVT}(U) = { a \mid U \stackrel{+}{\Rightarrow} \cdots a \text{或} U \stackrel{+}{\Rightarrow} \cdots aV, a \in V_t, \text{而} V \in V_n } $
LAST，以及在结尾非终结符前面的终结符
构造算法：
对于每条规则 $U ::= x_1 x_2 \cdots x_n$
- $x_i$ 和 $x_{i+1}$ 都为终结符号，$x_i = x_{i+1}$（终结符号挨在一起，$=$）
- $x_i$ 和 $x_{i+2}$ 都为终结符号, 但 $x_{i+1}$ 为非终结符号 THEN 置 $x_i = x_{i+2}$（终结符号非终结符号终结符号，两个终结符号相等）
- $x_i$ 为终结符号, 而 $x_{i+1}$ 为非终结符号，对 $FIRSTVT(x_{i+1})$ 中的每个 $b$ 置 $x_i < b$（终结符号非终结符号，该终结符号 $<$ 非终结符号的 FIRSTVT）
- $x_i$ 为非终结符号, 而 $x_{i+1}$ 为终结符号，$LASTVT(x_i)$ 中的每个 $a$，置 $a > x_{i+1}$（非终结符号终结符号，非终结符号的 LASTVT $>$ 终结符号）
- 如何理解：左边的是栈顶，所以每次生成算符，都是左边 $?$ 右边；然后，非终结符号的 FIRSTVT / LASTVT 更大。非终结符在前面，就取 LASTVT，在后面就取 FIRSTVT，总之是取和终结符挨得近的那个。
每次规约的是当前句型的最左素短语。素短语：至少包含一个终结符的短语，且不再包含其它素短语。

LR分析

活前缀：规范句型的前缀，并且不会超过一个句柄的最右端。

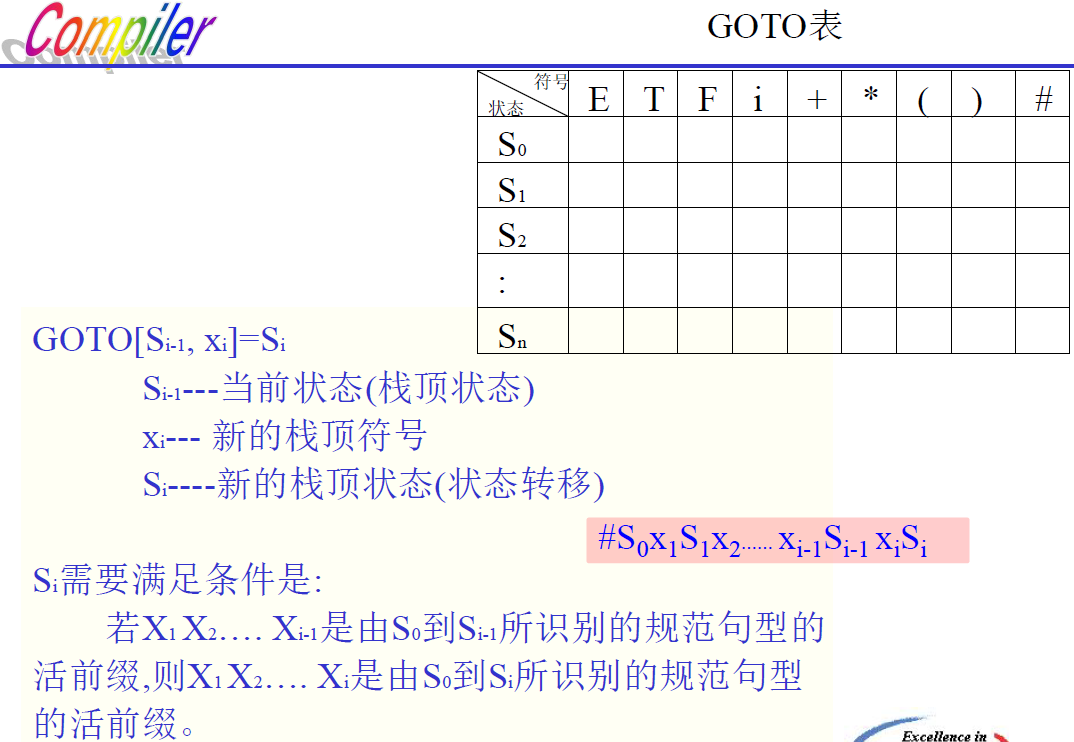
状态转移表（GOTO表）：

其实是个状态机。

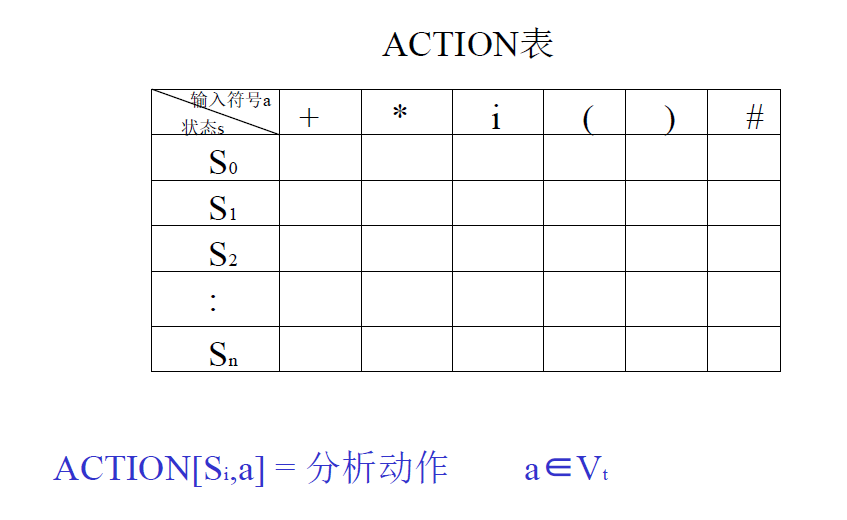
分析动作表（ACTION表）：

移进： $ \text{ACTION}[S_i, a] = s $
动作：将 $a$ 推进栈，并设置新的栈顶状态 $S_j$ $ S_j = \text{GOTO}[S_i, a] $，将指针指向下⼀个输入符号
归约： $ \text{ACTION}[S_i, a] = r_d $ $d$：文法规则编号 $(d) A \rightarrow \beta$
动作：将符号串 $\beta$ (假定长度为 $n$) 连同状态从栈内弹出，把 $A$ 推进栈，并设置新的栈顶状态 $S_j$
$ S_j = \text{GOTO}[S_{i-n}, A] $
接受： $\text{ACTION}[S_i, #] = \text{accept} $
出错：$ \text{ACTION}[S_i, a] = \text{error} $

根据 GOTO/ACTION进行规约/移进。

构造SLR分析表：

根据文法构造识别规范句型活前缀的有穷自动机 DFA，由 DFA 构造分析表。

构造DFA
确定S集合，即LR（0）项目集规范族，同时期确定 $S_0$。
- 构造 LR（0）
  LR（0）是DFA的状态集，每个状态是项目的集合。文法的每个产生式的右部添加一个圆点就构成一个项目。
  1. 将文法拓广，添加一个接受状态。
  2. 列出所有的项目
  3. 把有关项目组合成集合，即状态
- closure
- goto
求 ACTION 表
$k$ 是项目集（状态）
1、求出文法每个非终结符的FOLLOW集合
2、若项目 $A \rightarrow \alpha \cdot a \beta \in k$，且 $a \in V_t$，则置 $ \text{ACTION}[k, a] = s $ (移进)
3、若项目 $A \rightarrow \alpha \cdot \in k$，那么对输入符号 $a$，若 $a \in \text{FOLLOW}(A)$，则置 $\text{ACTION}[k, a] = r_j$ 其中 $A \rightarrow \alpha$ 为文法 $G’$ 的第 $j$ 个产生式。
4、若项目 $E’ \rightarrow E \cdot \in k$，则置 $\text{ACTION}[k, #] = \text{accept}$
5、ACTION 表中不能用步骤 2~4 填入信息的空白格，均置 error

判断是否是 SLR（1）文法：对于 $A \rightarrow \alpha \cdot \in k$，判断 FOLLOW（$A$）是否和 $k$ 中其它转移符号重合。

5 符号表

非分程序结构语言

非分程序结构语言：每个可独立编译的程序单元是一个不包含子模块的单一模块。

分全局符号表和局部符号表。

全局符号表：子程序、函数名、公共区变量
局部符号表：程序单元声明标识符
查表：先查局部符号表，再查全局符号表

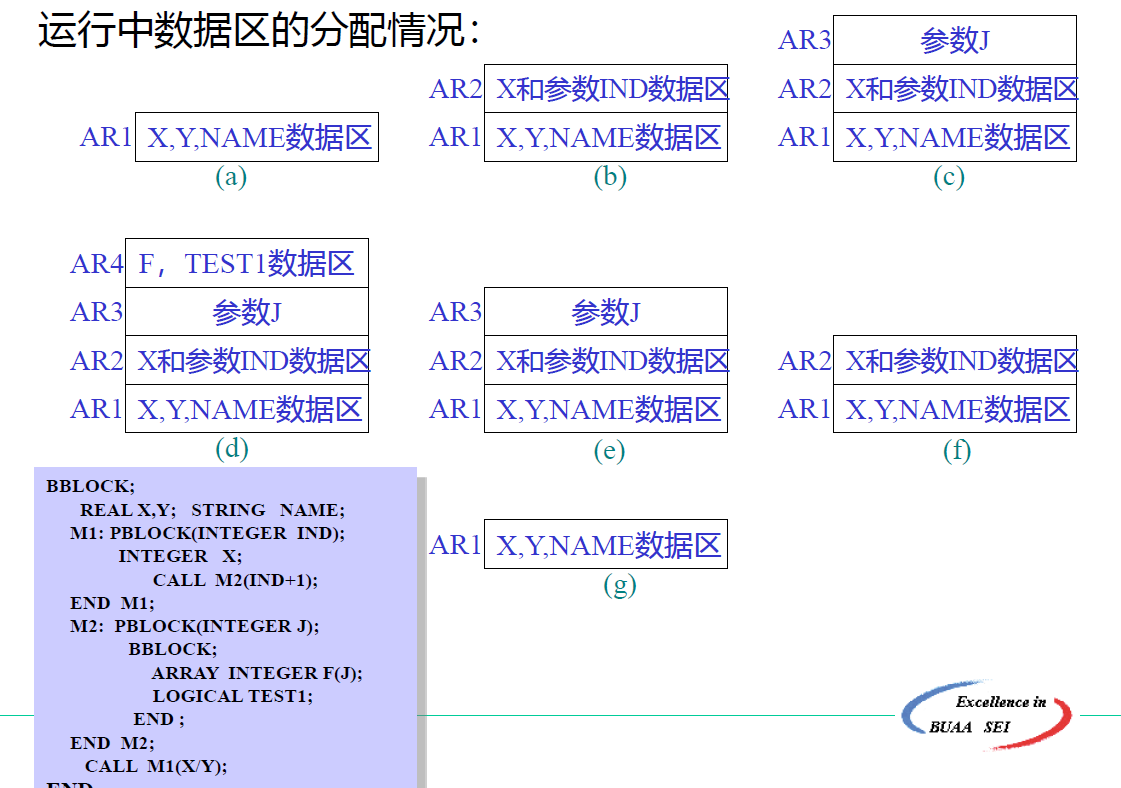
分程序结构语言

模块可以包含嵌套的子模块，每个子模块可以拥有自己的一组标识符。

查表：逐层向外查找

分程序的开始，执行定位操作；分程序结束，执行重定位操作。

BBLOCK：程序块的开始符号BEGIN，按顺序执行的程序块；

PBLOCK：过程块，通过调用来执行1，执行完之后返回调用点。

进入分程序，定位操作，建立子表，编译到分程序的结尾，删除符号表（重定位，使符号表恢复到进入分程序之前的情况）

6 运行时的存储组织及管理

运行栈：地址空间向下生长（高地址到低地址）

从子程序/函数返回时，当前运行栈将被废弃。

递归调用的同一个子程序/函数，每次调用将获得独立的运行栈空间。

运行栈包括：

函数返回地址
全局寄存器保护区
临时变量保护区
局部变量保护区
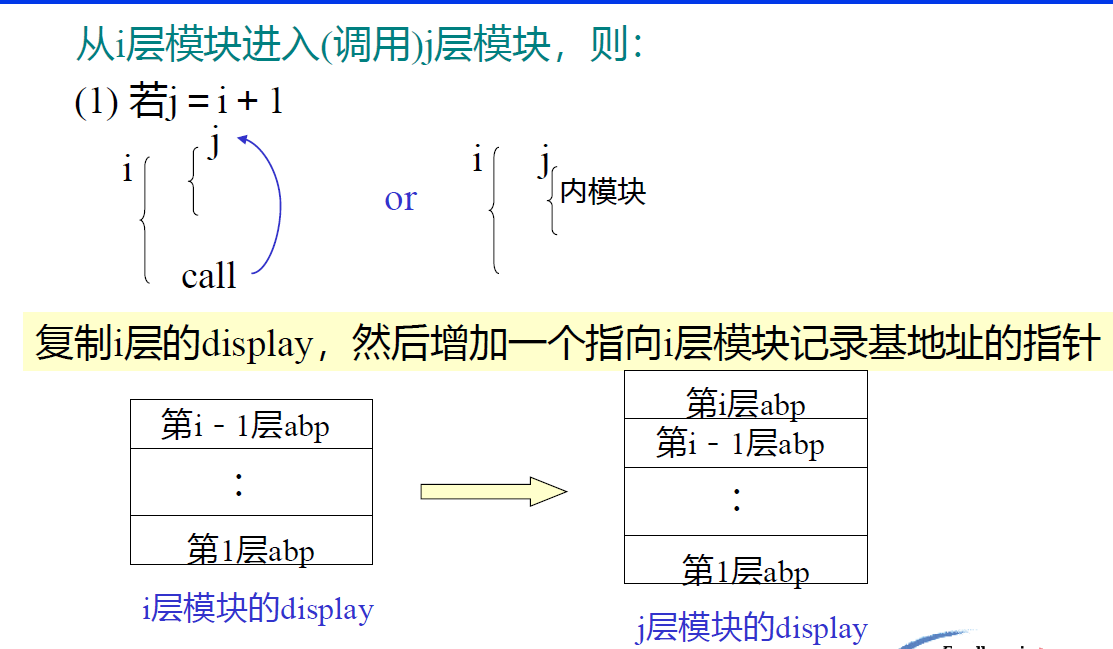
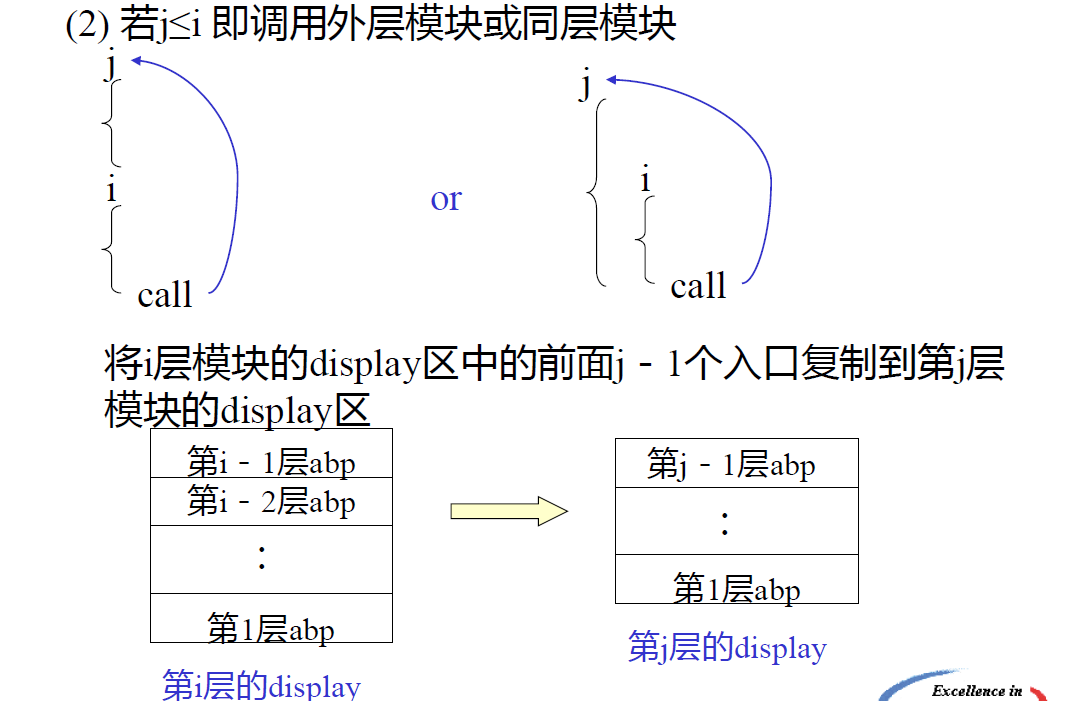
其他辅助信息（如 display）

静态存储分配：编译阶段管理。问题：不是所有数据空间大小都能在编译过程中确定。

动态存储分配：程序运行阶段由 目标程序 实现对存储空间的组织和管理。

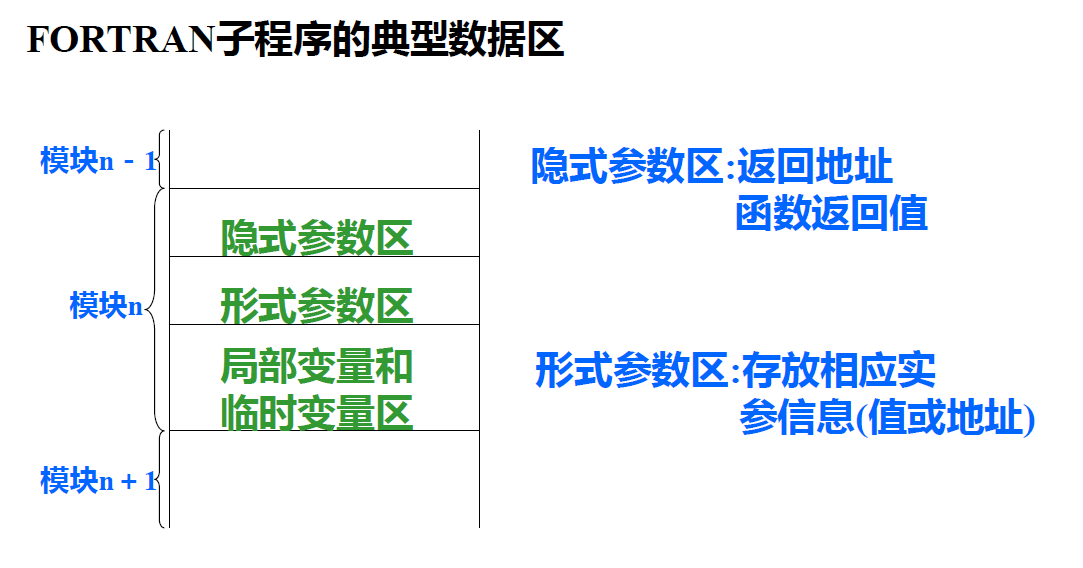
活动记录：分成三部分，局部数据区，参数区，display 区。

局部数据区：模块中定义的各个局部变量
参数区
- 显式参数区（出现在源程序中的 形参数据）
- 隐式参数区
  - prev abp：上一个 模块记录基地址，记录调用者信息
  - ret addr：返回地址，调用语句的下一条指令的地址
  - ret value：函数返回值
- display 区：存放 外层模块活动记录 的基地址

7 中间形式

波兰表示

后缀表达式，容易翻译，不容易优化。

转换方法：符号栈，如果栈顶优先级大于等于遇到的符号，就出栈并输出，否则符号入栈。

if 语句的波兰表示：if <expr> then <stmt_1> else [lable1] <stmt_2> [lable2]

波兰表示为 : <expr><label_1>BZ<stmt_1><label_2>BR<stmt_2>

BZ: 二目操作符，若的计算结果为0 (false)，则产生一个到的转移

BR: 一目操作符，产生一个到的转移

P-code

波兰表示的中间代码

运行P-code的抽象机没有专门的运算器或累加器，所有的运算(操作)都在运行栈的栈顶进行，如要进行d:=(a+b)*c的运算，生成P-code序列为：

取a  LOD a
取b  LOD b
+    ADD
取c  LOD c
*    MUL
送d  STO d

N-元表示

三元式：操作符左操作数右操作数

其中：

BMZ：测试第二个域的值，如果 $\leq 0$ 则转移到第三个域的地址，否则顺序执行
BR：转移到第三个域的地址

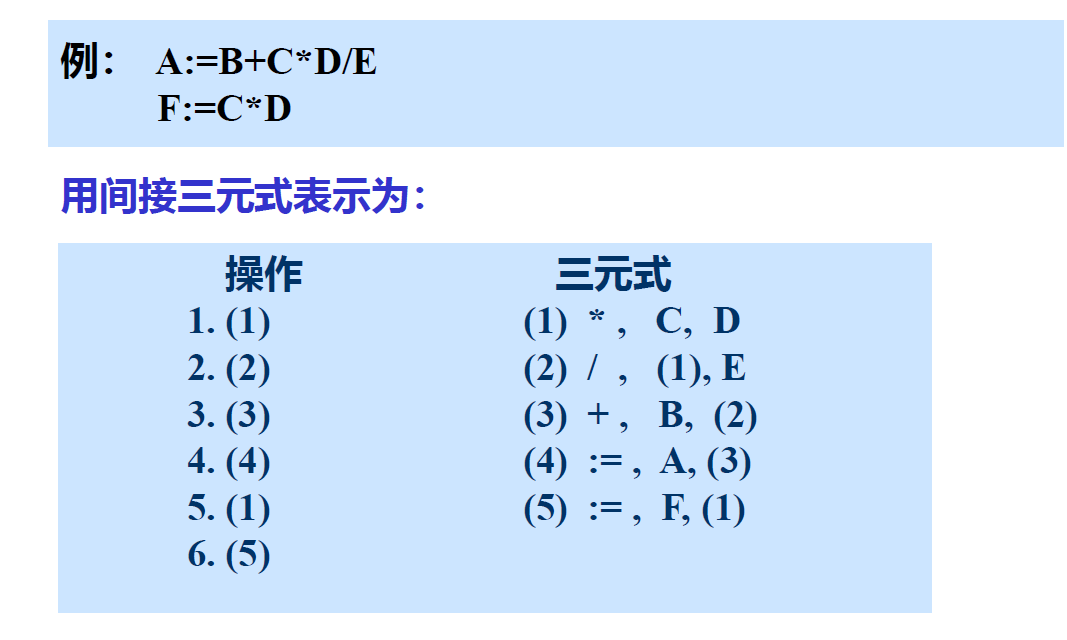
间接三元式：用另一张表表示执行次序。

四元式：操作符操作数1 操作数2 结果

结果 通常是临时变量。

8 错误处理

错误：语法错误，语义错误。

语法错误：不合文法

语义错误：

语义规则：
- 标识符先说明后引用
- 标识符引用要符合作用域规定
- 过程调用时实参与形参类型要一致或兼容
- 参与运算的操作数类型一致或兼容
- 下标变量下标不能越界
超越系统限制：
- 数据溢出错误
- 符号表、静态存储分配数据区溢出
- 动态存储分配数据区溢出

错误侦察：编译程序侦察违反语法和语义规则以及超越编译系统限制的错误；目标程序在运行时侦察下标越界，计算结果溢出以及动态存储数据区溢出。

错误报告：分析完后报告 or 边分析边报告

错误处理：错误改正；错误局部化处理（把错误的影响限制在一个局部的范围，避免影响程序其它部分的分析）

错误局部化处理

一般原则
侦察到错误后，暂停对后面符号的分析，跳过错误所在的语法成分继续向下分析（词法分析跳过单词，语法语义分析跳过语句右界，从新语句开始分析）。
实现：递归下降分析法
发现错误，先存储错误信息，然后进行错误处理：跳过一段源程序，直到跳到语句的右界或正在分析的语法成分的合法后继符号。

目标程序运行时错误：打印错误信息和运行现场，然后停止程序运行。

9 语法制导翻译技术

输入文法：未插入动作符号的文法，可以推导产生输入序列。

翻译文法：插入动作符号的文法，可以推导产生 活动序列（输入序列 + 动作序列，由终结符和动作符号组成）。

语法制导翻译：按翻译文法进行的翻译，根据翻译文法获得动作序列，并执行动作序列的动作。

属性翻译文法

综合属性：属性的计算是自右向左，自底向上 的

继承属性：可以从前文得到，继承前面的值。属性求值是自左向右，自顶向下 的。

L-属性翻译文法 L-ATG

文法中的终结符，非终结符及动作符号都带有属性，且每个属性都有一个值域。
非终结符及动作符号的属性可分为继承属性和综合属性。
开始符号的继承属性具有指定的初始值。
输入符号（终结符号）的每个综合属性具有指定的初始值。
属性的求值规则：
- 继承属性：产生式左部的非终结符取 前面的产生式右部 该符号的继承属性值；产生式右部的继承属性值取 该产生式左部符号 的继承属性值或 该符号左部 的属性值。
- 综合属性：产生式右部非终结符取 后面的产生式左部 同名非终结符的综合属性值；产生式左部非终结符取 该符号的继承属性 或 某个右部符号的属性；动作符号取该符号的继承属性或某个右部符号的属性。（即要么往右部继续向下递归找，要么取继承属性）

简单赋值形式的L-属性翻译文法 SL-ATG

产生式右部符号的继承属性是常量
产生式左部非终结符号的综合属性是常量

如何把 L-ATG 转换成等价的 SL-ATG？

引入新的动作符号表示函数求值，并引入新的产生式。把动作符号插入可以放的位置的最左边（保证动作符号的继承属性都在符号左边，且用到动作符号的综合属性的符号在动作符号的右边）

10 语义分析代码生成这个好像不考

语义分析：构建符号表

栈式抽象机：

三个存储器
- 数据存储器
- 操作存储器
- 指令存储器
指令存储器
地址存储器

12 目标代码生成

指令集架构：

栈式架构
寄存器-寄存器架构

运行栈：

函数返回地址
全局寄存器
临时变量
未分配到全局寄存器的局部变量
其它辅助信息（如 display）

寄存器分配

全局变量/静态变量不参与全局寄存器分配，寄存器专属于线程。

问题：怎么构建变量冲突图？？？

图着色算法：

有 $k$ 个全局寄存器，就用 $k$ 种颜色染色，让图中相邻点颜色都不相同。

找第一个连接边数目 小于 k 的点，移走
重复 1，直到没有点可以被移走
取一个点，记录为“不分配全局寄存器”，移走
重复 1-3，直到只剩一个点
按照节点被移走的顺序，反向加边加点，每次加点选合适的颜色放进去

13 代码优化

划分基本块

标记“入口语句”
- 第一条语句
- 跳转语句跳转到的语句
- 跳转语句后的第一条语句
每个入口语句到下一个入口语句，是一个基本块

流图

有向图，节点是基本块。

B1 → B2：

B1 最后一条语句可以转移到 B2 的第一条语句
B2 在 B1 后，且 B1 最后没有无条件转移去其它基本块

A 是 B 的必经节点，A dom B，从首节点出发任何到 B 的路径都要经过 A。

如果有边 B → A 且 A dom B，则这个边是循环的回边。

基本块的 DAG 图

构建方法：

对于 $z = x\ \text{op}\ y$ ，首先在节点表里找 $x,y$，如果找不到就新建节点并加入节点表中。假设最后节点表中对应关系有 $(x, y) = (i, j)$
找有没有名为 $\text{op}$ 的中间节点，且左右节点标记分别为 $i, j$，如果没有的话，新建中间节点。假设最后找到或新建的中间节点编号为 $k$
在节点表里找 $z$，如果有的话就更新为 $k$，如果没有的话就加入到节点表中。

从 DAG 导出中间代码

不断选择 所有父节点均已进入队列 的中间节点，将它加入列表，然后递归下去访问它的最左子节点，直到某个最左子节点不满足所有父节点均进入队列，然后再去找符合要求的中间节点。

把中间节点队列逆序输出，得到中间结点的计算顺序，整理成中间代码序列。

到达定义数据流方程

$in[B] = \cup_{P \in pred[B]} out[P]$，$out[B] = gen[B] \cup (in[B] - kill[B])$

$kill[B] = kill[d_1] \cup kill[d_2] \cup \ldots \cup kill[d_n]$，$d_1 \sim d_n$ 依次为基本块中的语句

$gen[B] = gen[d_n] \cup (gen[d_{n-1}] - kill[d_n]) \cup (gen[d_{n-2}] - kill[d_{n-1}] - kill[d_n]) \cup \ldots \cup (gen[d_1] - kill[d_2] - kill[d_3] \ldots - kill[d_n])$

kill 和 gen 是一开始就要算出来的，然后不断更新 in 和 out 直到稳定。

活跃变量分析

$in[B] = use[B] \cup (out[B] - def[B])$
$out[B] = \cup_{\text{B的后继基本块P}} in[P]$
$def[B]$：变量在B中被定义（赋值）先于任何对它们的使用
$use[B]$：变量在B中被使用先于任何对它们的定义

先求 def 和 use，然后不断更新 in 和 out 直到稳定。

冲突图：变量定义点的基本块的 in 和该变量冲突。

定义-使用链

变量的某一定义点，以及所有可能使用该定义点所定义变量值的使用点所组成的一个链。

期末复习, 编译原理

编译原理期末复习

This post is licensed under CC BY 4.0 by the author.