2024秋 最优化（运筹学） 期末复习
2024秋 计算机工程中最优化的方法（运筹学） 期末复习笔记
最优化
单纯形算法
等式形式的线性规划模型
对问题约束施加两个要求：
- 都是等式，且右端项非负
- 所有变量非负
解题过程：
- 确定决策变量
- 确定目标函数
- 构造约束条件
- 增加非负 松弛变量，必要时在方程两端乘 $-1$，把不等式转换为带有非负右端项的等式约束
最优解的候选解是 有限个基本可行解（对应图像上的一个角点）。
假设最后的方程组有 $m$ 个方程和 $n$ 个变量，每个基本可行解对应 $n-m$ 个变量为 $0$ 的一个解。这 $n-m$ 个零变量为 非基变量，剩下 $m$ 个变量为 基变量，它的解称为 基本解。
单纯形方法
考察所有角点中的一小部分，查找最优角点。
进基变量：进入基本可行解的变量
离基变量：离开基本可行解的变量
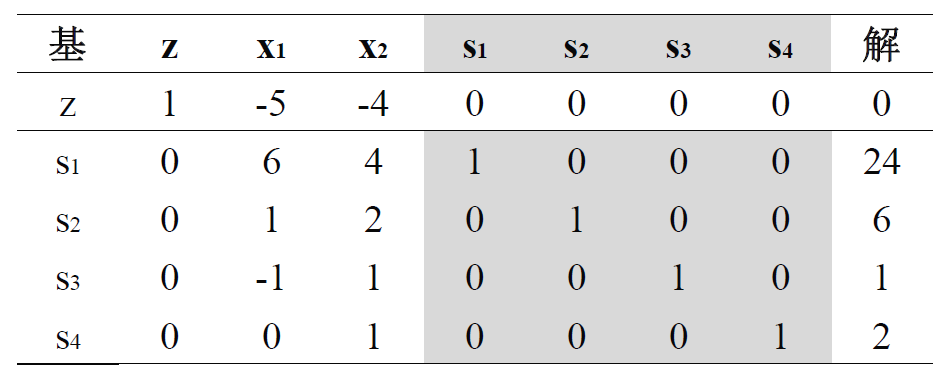
例子： \(\text{max} \quad z = 5x_1 + 4x_2 + 0s_1 + 0s_2 + 0s_3 + 0s_4\)
\[\text{s.t.} \quad \begin{aligned} & 6x_1 + 4x_2 + s_1 = 24 \\ & x_1 + 2x_2 + s_2 = 6 \\ & -x_1 + x_2 + s_3 = 1 \\ & x_2 + s_4 = 2 \\ & x_1, x_2, s_1, s_2, s_3, s_4 \geq 0 \end{aligned}\]初始单纯形表（画出表之后注意看一下目标方程所在行中，基变量对应的系数是否均为 $0$，如果不是，则要与对应的基变量行相加减，使它的系数为 $0$）：
初始基本解为松弛变量，非基变量（不在基列中）总是等于 $0$。
确定进基变量：进基变量应为 目标方程（移项得到右项为零的等式）中具有 最负系数 的变量。（本来应该选最正的，但是移项之后系数变了，所以选最负的）（如果目标函数是求最小值，那就选最正系数）
- 确定离基变量：计算右端项（“解”）与进基变量下方的约束系数的 非负比，选取 最小非负比 的基变量为离基变量。
- 令枢轴元素为 $1$，且除枢轴行外，枢轴列其它元素为 $0$（有点像高代的消元啥的）。
- 重复寻找进基变量，直到目标方程没有负系数（求最小值则为正系数）为止。
改进单纯形方法
带有 $=$ 和 $\ge$ 约束：使用在最初迭代中扮演松弛变量角色的人工变量，然后在迭代中对他们进行处理。
大 M 方法
如果第 $i$ 个等式约束和没有松弛变量，那么将人工变量 $R_i$ 加入到初始解中作为松弛变量充当初始基本解。
人工变量不是原始模型的一部分，因此需要在目标函数中对他们制定极高的惩罚，强迫他们在最优解中等于 $0$。
用一个“充分大的正数” $M$ 来构建人工变量的目标系数。
例子： \(\text{min} \quad z = 4x_1 + x_2\)
\[\text{s.t.} \quad \begin{aligned} & 3x_1 + x_2 = 3 \\ & 4x_1 + 3x_2 \geq 6 \\ & x_1 + 2x_2 \leq 4 \\ & x_1, x_2 \geq 0 \end{aligned}\]先转换为等式形式： \(\text{min} \quad z = 4x_1 + x_2\)
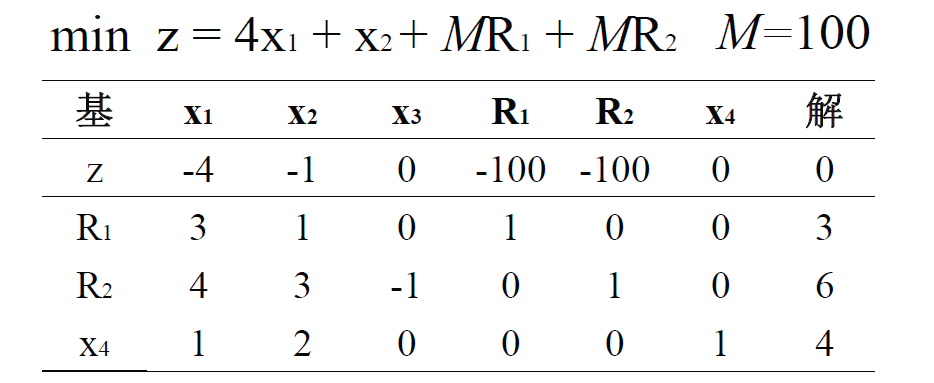
\[\text{s.t.} \quad \begin{aligned} & 3x_1 + x_2 = 3 \\ & 4x_1 + 3x_2 - x_3 = 6 \\ & x_1 + 2x_2 + x_4 = 4 \\ & x_1, x_2, x_3, x_4 \geq 0 \end{aligned}\]前两个方程没有松弛变量，增加人工变量 $R_1, R_2$，并修改目标函数。 \(\text{min} \quad z = 4x_1 + x_2 + MR_1 + MR_2\)
\[\text{s.t.} \quad \begin{aligned} & 3x_1 + x_2 + R_1 = 3 \\ & 4x_1 + 3x_2 - x_3 + R_2 = 6 \\ & x_1 + 2x_2 + x_4 = 4 \\ & x_1, x_2, x_3, x_4, R_1, R_2 \geq 0 \end{aligned}\]$M$ 相对于初始目标系数一定是充分大，迫使人工变量在最优解中取到 $0$。
得到初始表：
注意到初始解为 $(R_1, R_2, x_4) = (3, 6, 4)$，$z$ 行结果与右端项不相等，主要是因为初始基变量在 $z$ 行有非零系数导致的。因此让 $z$ 行与相应的 $R_1, R_2$ 行进行加减，消去系数，最后用正常的单纯形方法求解即可。
如果没有可行解，最终的单纯形表将至少包含一个人工变量取正值。
问题：惩罚值 $M$ 需要很大，可能造成计算精度降低。
两阶段法
分两个阶段求解：求初始基本可行解；求解原问题。
- 阶段 1：将问题变成等式约束形式，并增加必要的人工变量。然后把问题转换为将 人工变量之和最小化 的问题（不管原问题是求极大还是极小，都求最小），得到这个问题的基本解以及和的最小值，如果和的最小值为正，无可行解，否则进行阶段 2。
- 阶段 2：用阶段 1 得到的基本解作为初始可行解。
例子：
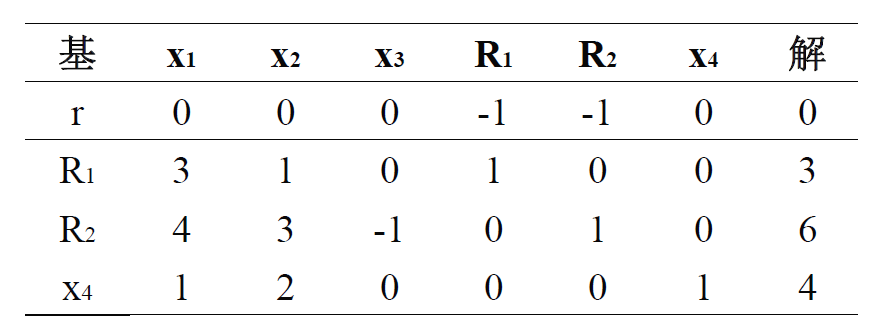
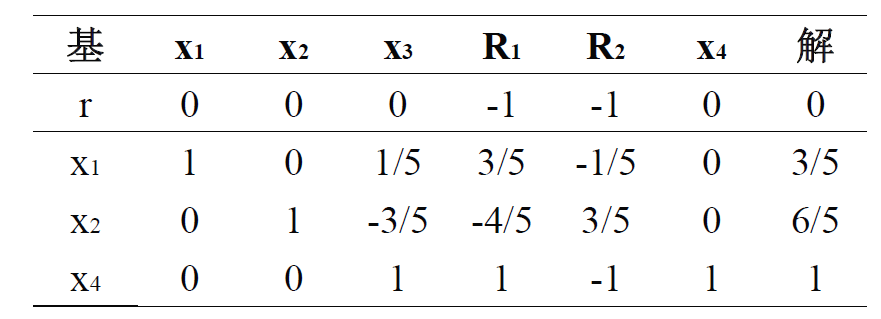
第一阶段开始，对于初始约束转换成的等式形式，先添加人工变量和松弛变量，尝试求解人工变量和的最小值： \(\text{min} \quad r = R_1 + R_2\)
\[\text{s.t.} \quad \begin{aligned} & 3x_1 + x_2 + R_1 = 3 \\ & 4x_1 + 3x_2 - x_3 + R_2 = 6 \\ & x_1 + 2x_2 + x_4 = 4 \\ & x_1, x_2, x_3, x_4, R_1, R_2 \geq 0 \end{aligned}\]初始表：
初始基变量在目标方程行有非零系数，这导致 $r$ 与右端项并不相同，需要先把初始基变量消去，得到正确的表，之后用单纯形方法求解这个问题，得到最终表格：
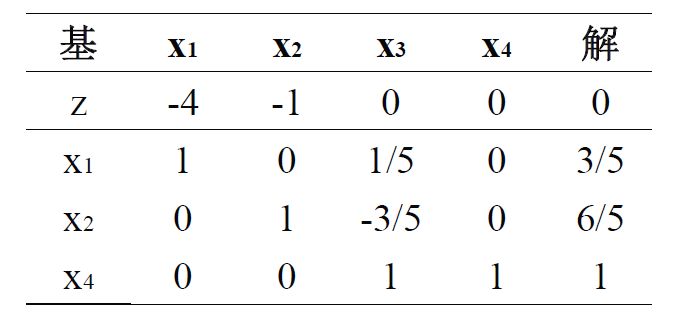
产生基本可行解 $(x_1, x_2, x_4) = (3/5, 6/5, 1)$，去除人工变量列，转入阶段 2，得到阶段 2 的原始问题： \(\text{min} \quad z = 4x_1 + x_2\)
\[\text{s.t.} \quad \begin{aligned} & x_1 + \frac{1}{5}x_3 = \frac{3}{5} \\ & x_2 - \frac{3}{5}x_3 = \frac{6}{5} \\ & x_3 + x_4 = 1 \\ & x_1, x_2, x_3, x_4 \geq 0 \end{aligned}\]初始表：
初始基变量在目标方程行有非零系数，这导致 $r$ 与右端项并不相同，需要先把初始基变量消去，得到正确的表，之后用单纯形方法求解这个问题即可。
作业
作业 1
\[\text{max} \quad z = 2x_1 + 3x_2\] \[\text{s.t.} \quad \begin{aligned} & x_1 + 2x_2 \leq 8 \\ & 4x_1 \leq 16 \\ & 4x_2 \leq 12 \\ & x_1, x_2 \geq 0 \end{aligned}\]作业 2
用两阶段方法求解： \(\text{min} \quad z = 4x_1 + x_2\)
\[\text{s.t.} \quad \begin{aligned} & 3x_1 + x_2 \leq 3 \\ & 4x_1 + 3x_2 \geq 6 \\ & x_1 + 2x_2 \leq 4 \\ & x_1, x_2 \geq 0 \end{aligned}\]对偶理论与灵敏度分析
灵敏度分析
==todo：感觉不会考，有空再看==
对偶理论
一个问题的最优解自动提供另一个问题的最优解。
对偶变量对应每个原始约束，对偶约束对应每个原始变量，对偶约束的右端项对应原始目标函数的相应变量系数，对偶目标系数对应原始问题约束方程的右端项。
简单而言，就是竖过来看。
原始问题极大化，对偶问题极小化，约束为 $\ge$，反之亦然。
举例说明：
原始问题： \(\text{max} \quad z = 5x_1 + 12x_2 + 4x_3\)
\[\text{s.t.} \quad \begin{aligned} & x_1 + 2x_2 + x_3 \leq 10 \\ & 2x_1 - x_2 + 3x_3 = 8 \\ & x_1, x_2, x_3 \geq 0 \end{aligned}\]等式方程形式的原始问题：
\[\text{max} \quad z = 5x_1 + 12x_2 + 4x_3 + 0x_4\] \[\text{s.t.} \quad \begin{aligned} & x_1 + 2x_2 + x_3 + x_4 = 10 \quad (y_1) \\ & 2x_1 - x_2 + 3x_3 = 8 \quad (y_2) \\ & x_1, x_2, x_3 \geq 0 \end{aligned}\]对偶问题： \(\text{min} \quad w = 10y_1 + 8y_2\)
\[\text{s.t.} \quad \begin{aligned} & x_1 + 2x_2 \geq 5 \\ & 2x_1 - x_2 \geq 12 \\ & x_1 + 3x_2 \geq 4 \\ & x_1 \geq 0 \\ & x_1, x_2 \quad \text{无限制} \end{aligned}\]作业
原始问题：
\[\text{min} \quad z = 7x_1 + 9x_2 + 10x_3\] \[\text{s.t.} \quad \begin{aligned} & x_1 - 2x_3 \leq 8 \\ & 2x_2 - 8x_3 \geq 1 \\ & x_1, x_2, x_3 \geq 0 \end{aligned}\]求对偶问题。
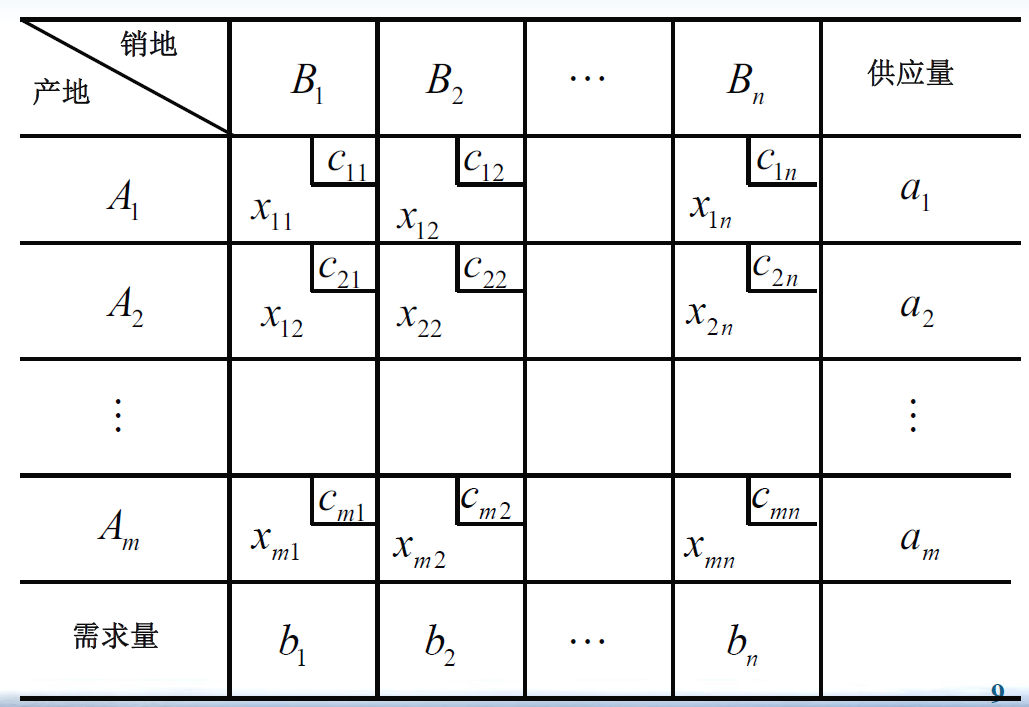
运输问题
$m$ 个起点和 $n$ 个终点，每个起点有一个供应量 $a_i$，每个终点有一个需求量 $b_j$，每个起点 $i$ 到每个终点 $j$ 都有一个边，记录了运输费用 $c_{ij}$ 和 运输量 $x_{ij}$。求运输总费用最小。
可以用单纯形方法求解，但用运输表来求解更方便。
运输算法假定了总供应量与总需求量相等，如果不等，可以增加一个虚设起点或虚设终点来让模型平衡，虚点的运输费用为 $0$。
生产-库存问题也可以建模成运输问题。
运输算法
确定一个基本的可行解
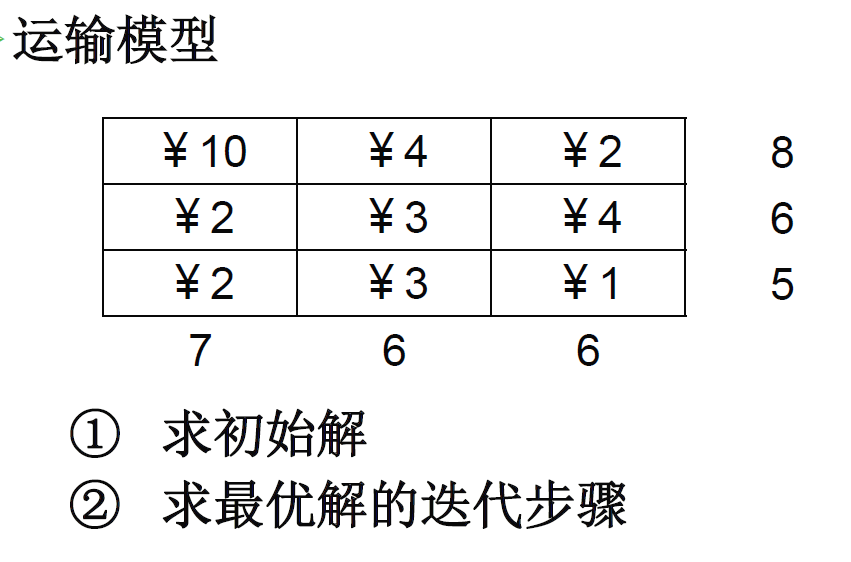
西北角法
从表中西北角（左上）的元素开始，取这个元素对应的供应和需求的值的 $\min$，然后供应和需求都减这个值，$x_{ij}$ 也取这个值。删除零供应的行或零供应的列（若均为零，只删一个），如果删的是行，元素转到下面，如果删的是列，元素转到右边。直到恰好剩下一行或一列没有被删除。
最小费用法
Vogel 近似法
利用单纯形方法的最优性条件，在所有非基变量中确定进基变量，如果最优条件满足，停止，否则，转到第三步
对于每一个基变量（已有确定的 $x_{ij}$），列出式子 $u_i + v_j = c_{ij}$，然后令 $u_1 = 0$，就可以求出其他项。 然后对每个非基变量求 $z_{ij} = u_i + v_j - c_{ij}$，取最正系数的 $z$ 变量作为入基变量。
利用单纯形方法的可行性条件，在所有现有的基变量中确定离基变量，寻求新的基本解，返回到第二步。
假设进基变量 $x_{ij}$ 运输 $\theta$ 个单位，求 $\theta_{\max}$：
找三个基变量，和 $x_{ij}$ 围成一个矩形，然后把 $\theta$ 分配进去，根据下列条件得到不等式组：
- 满足供应上限、需求约束
- 所有路径运输量非负
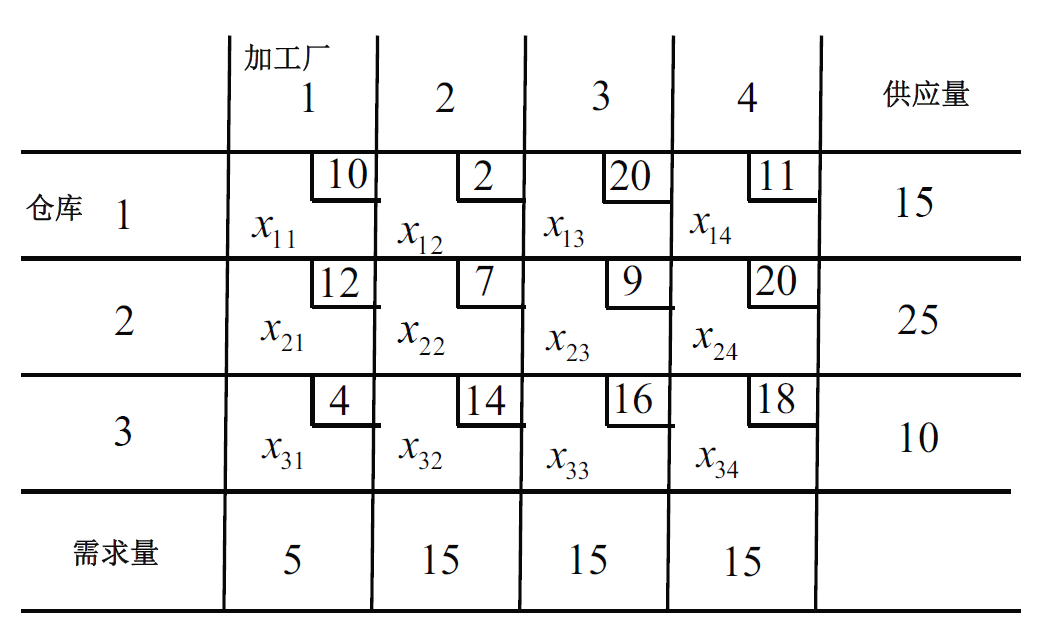
例题：
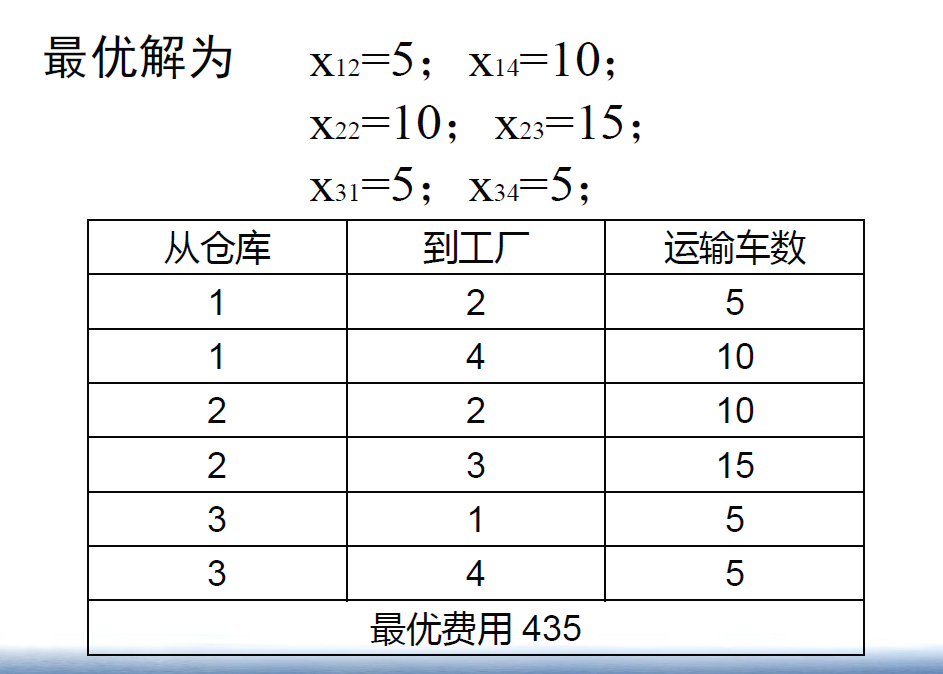
西北角法的初始基本解为： \(x_{11} = 5; \quad x_{12} = 10;\)
\[x_{22} = 5; \quad x_{23} = 15;\]
作业
目标规划
线性规划：优化单个目标函数。
如何优化多个目标？
目标规划：根据各个目标的相对重要程度，寻找一个折中的解。
假如有一堆不等式，每个不等式对应一个目标，这些不等式可能不能同时满足，因此可以把不等式转化为一个弹性目标。
例子： \(550x_p + 35x_f + 55x_s + 0.075x_g \geq 16\)
\[35x_f \leq 0.1(550x_p + 35x_f + 55x_s + 0.075x_g)\] \[55x_s \leq 0.2(550x_p + 35x_f + 55x_s + 0.075x_g)\] \[x_g \leq 2\]转化为弹性目标： \(550x_p + 35x_f + 55x_s + 0.075x_g + S_1^- - S_1^+ = 16(\ge)\)
\[55x_p - 31.5x_f + 5.5x_s + 0.0075x_g + S_2^- - S_2^+ = 0(\ge)\] \[110x_p + 7x_f - 44x_s + 0.015x_g + S_3^- - S_3^+ = 0(\ge)\] \[x_g + S_4^- - S_4^+ = 2(\le)\]非负变量 $S_i^+, S_i^-$ 表示第 $i$ 个约束中低于和高于右端项的一种便宜程度，称作 偏离变量。$S_i^+$ 和 $S_i^-$ 是相关的，不能同时作为基变量，因此每次只有一个能被赋值为整数（另一个是零）。
对于 $\le$，如果其 $S_i^- > 0$，则第 $i$ 个目标满足；否则不满足。反之亦然。
折中解就是尽量满足，另一个尽可能都取 $\min$。
权和法：就是最小化那个应尽可能取 $\min$ 的变量加权和。
整数规划
要求某些或全部的变量只取整数值（或离散值）的线性规划。
会列式子就行，一般是取（$0\ \text{or}\ 1$）。
动态规划
背包模型：
对能装$n$件物品、$W$千克的背包问题，建立一个后向递归方程。令$m_i$为背包中物品$i$的数量，定义$r_i$和$w_i$分别是每单位物品$i$的收益和重量：
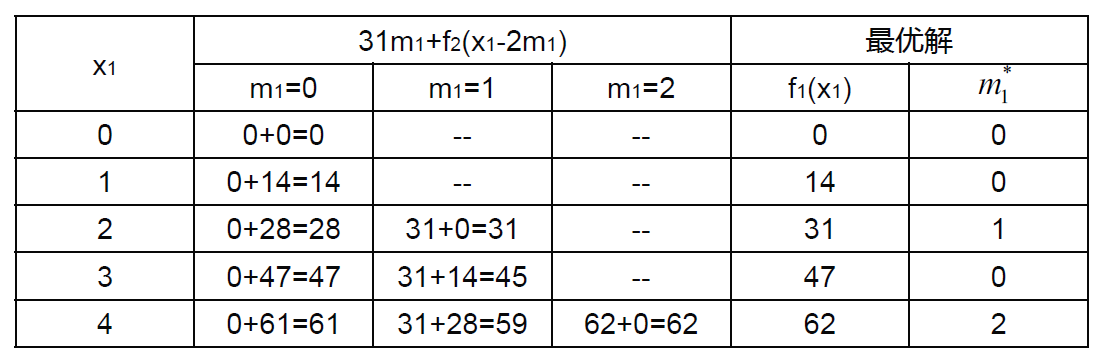
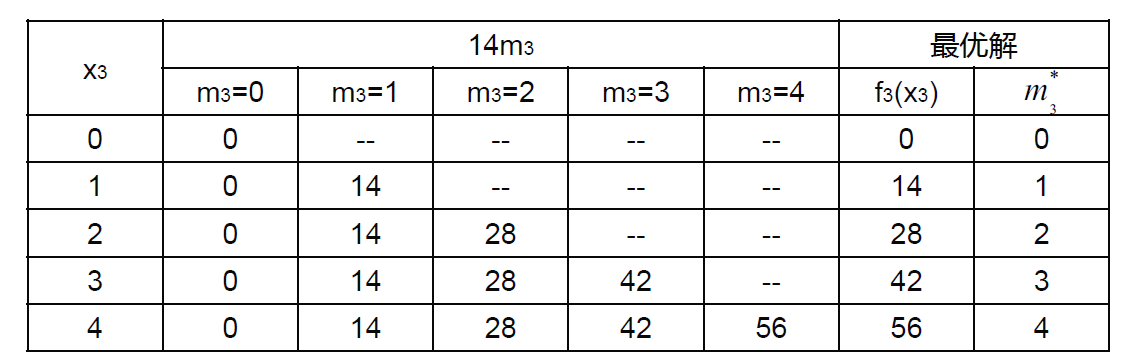
\[\text{max} \quad z = r_1m_1 + r_2m_2 + \cdots + r_nm_n\] \[\text{s.t.} \quad w_1m_1 + w_2m_2 + \cdots + w_nm_n \leq W\] \[m_1, m_2, \ldots, m_n \geq 0 \quad \text{并且为整数}\]从物品 $n$ 往前放，$x_i$ 表示放到物品 $i$ 时，背包里物品的总重量，$\text{f}_i(x_i)$ 表示考虑物品 $i-n$，背包里物品总重量为 $x_i$ 时的最大收益。 \(f_i(x_i) = \max_{m_i = 0, 1, \ldots, \left\lfloor \frac{W}{w_i} \right\rfloor} \left\{ r_im_i + f_{i+1}(x_i - w_im_i) \right\}\) 例题：
一艘载货量4吨的货船可装载3种货物，下表给出每种货物$i$的单位重量$w_i$（吨）以及单位收益$r_i$（万元），该货船应如何装载这些货物才能获得最大收益？
| 货物$i$ | $w_i$ (吨) | $r_i$ (万元) |
|---|---|---|
| 1 | 2 | 31 |
| 2 | 3 | 47 |
| 3 | 1 | 14 |
\(f_2(x_2) = \max_{m_2 = 0, 1} \{47m_2 + f_3(x_2 - 3m_2)\}\)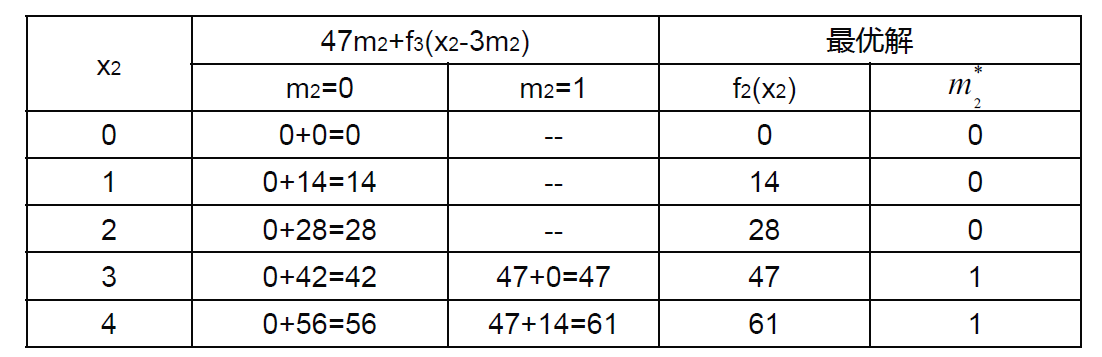 
\(f_1(x_1) = \max_{m_1 = 0, 1, 2} \{31m_1 + f_2(x_1 - 2m_1)\}\) 