2024秋 算法设计与分析 理论复习
2024秋 算法设计与分析
伪代码书写约定
递归式分析:主定理
主定理: 对形如 $T(n) = aT\left(\frac{n}{b}\right) + f(n)$ 的递归式
\[T(n) = \begin{cases} \Theta(f(n)) & \text{if } f(n) = \Omega(n^{\log_b a + \epsilon}) & \text{①}\\ \Theta(n^{\log_b a} \log n) & \text{if } f(n) = \Theta(n^{\log_b a}) & \text{②}\\ \Theta(n^{\log_b a}) & \text{if } f(n) = O(n^{\log_b a - \epsilon}) & \text{③} \end{cases}\]正则条件:若存在常数 $\epsilon > 0$ 使 $f(n) = \Omega(n^{\log_b a + \epsilon})$,且存在常数 $c \leq 1$ 和足够大的 $n$,使得 $af\left(\frac{n}{b}\right) \leq cf(n)$,则 $T(n) = \Theta(f(n))$。(保证根节点代价大于下一层代价之和)
主定理(简化形式): 对形如 $T(n) = aT\left(\frac{n}{b}\right) + n^k$ 的递归式
\[T(n) = \begin{cases} \Theta(n^k) & \text{if } k > \log_b a & \text{①} \\ \Theta(n^k \log n) & \text{if } k = \log_b a & \text{②} \\ \Theta(n^{\log_b a}) & \text{if } k < \log_b a & \text{③} \end{cases}\]主定理(扩展形式): 对形如 $T(n) = aT\left(\frac{n}{b}\right) + f(n)$ 的递归式
\[T(n) = \begin{cases} \Theta(f(n)) & \text{if } f(n) = \Omega(n^{\log_b a + \epsilon}) & \text{①} \\ \Theta(n^{\log_b a} \log^{k+1} n), \, k \geq 0 & \text{if } f(n) = \Theta(n^{\log_b a} \log^k n) & \text{②} \\ \Theta(n^{\log_b a}) & \text{if } f(n) = O(n^{\log_b a - \epsilon}) & \text{③} \end{cases}\]情况②的三种扩展 \(T(n) = \begin{cases} \Theta(n^{\log_b a} \log^{k+1} n) & \text{if } k > -1 \\ \Theta(n^{\log_b a} \log \log n) & \text{if } k = -1 \\ \Theta(n^{\log_b a}) & \text{if } k < -1 \end{cases} \quad \text{②}\)
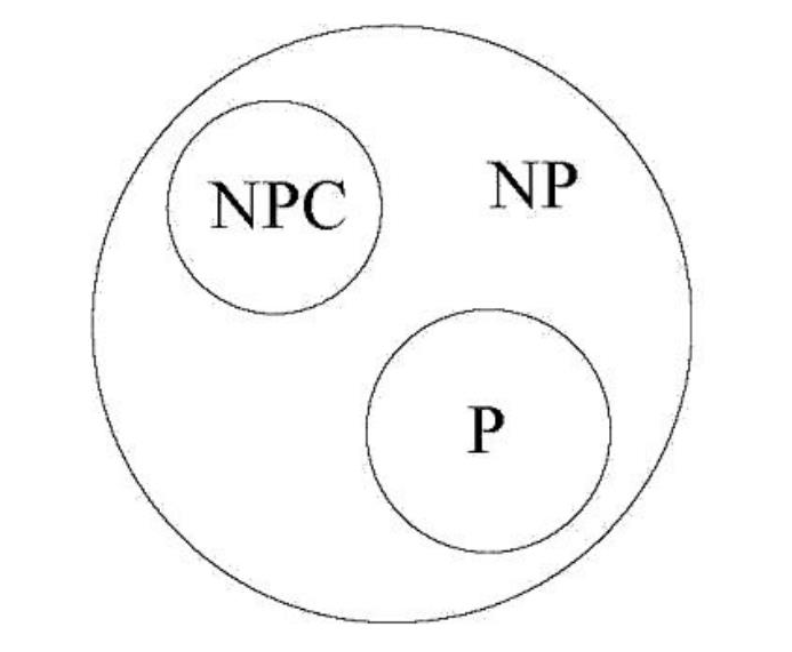
P, NP, NPC
NP-complete 问题:当前未找到一种解决方案,如果找到了,那么所有 NP-complete 问题都可以被解决。
问题:如何证明一个问题是 NP-complete 的。
P, NP
一个问题的复杂度由输入的规模来决定。如何编码输入?任何问题的输入都可以编码为二进制串。
问题输入的大小:编码问题输入所需要的最小 bit 数。选择一种简单的编码方式即可。
决策问题:一个问题有两种可能的答案(是或不是)。L 是问题,x 是输入,$x \in L$ 表示答案为是,$x \notin L$ 表示答案为不是。
优化问题:答案是一个最优解。优化问题一般会有一个对应的决策问题。
复杂度分类:
- easy
- hard
- hardest
如何对决策问题进行分类:使用多项式时间算法。
多项式时间复杂度算法:$O(n^k)$,注意 $n$ 是指输入的规模。
如果问题存在多项式时间复杂度算法,就说明这个问题是可解的。
P 类问题:存在多项式时间复杂度做法的决策问题。
例子:判断图是否是树,求图的最小生成树
证书:对应于一个 yes-input,以证明这个 input 是一个 yes-input.
验证证书:用这个证书来验证一个 input 确实是一个 yes-input.
NP(非确定性多项式时间)类问题:对于每个 yes-input,都存在一个证书可以在多项式时间内验证其确实是一个 yes-input。
例子:判断一个数是否是合数,判断集合中是否存在一个子集使得和为某个数,顶点覆盖问题(求一个点集覆盖所有边)
SAT 问题:确定一个布尔公式是否是可满足的(找到一组变量值,使得结果为真)。
证书由变量的一组赋值组成,验证证书的复杂度是 $O(n)$.
NPC
规约:问题之间的一种关系。如果问题 Q 的每一个实例都可以重新表述为问题 Q’ 的一个实例,则问题 Q 可以规约为问题 Q’。
多项式时间归约(Polynomial-Time Reductions)
设 $L_1$ 和 $L_2$ 是两个决策问题。
从 $L_1$ 到 $L_2$ 的 多项式时间归约 是一个变换函数 $f$,满足以下两个性质:
- $f$ 将 $L_1$ 的输入 $x$ 转换为 $L_2$ 的输入 $f(x)$,并满足:
- $L_1$ 的“是”输入被映射到 $L_2$ 的“是”输入,
- $L_1$ 的“否”输入被映射到 $L_2$ 的“否”输入。
- $f(x)$ 在输入大小 $\text{size}(x)$ 上可以在多项式时间内计算。
如果存在这样的 $f$,则称 $L_1$ 可以多项式时间归约到 $L_2$,记作:
\[L_1 \leq_P L_2\]如果 $L_1 \leq_P L_2$ 且 $L_2 \in \mathcal{P}$,则 $L_1 \in \mathcal{P}$。
如果 $L_1 \leq_P L_2$ 且 $L_2 \leq_P L_3$,则 $L_1 \leq_P L_3$。
NP 完全问题(NPC)
类 NPC(NP-complete)问题包括所有满足以下条件的决策问题 $L$:
- $L \in \mathcal{N}\mathcal{P}$;
- 对于任意 $L’ \in \mathcal{N}\mathcal{P}$,$L’ \leq_P L$。
- 直观上,NPC 包含 NP 中所有最难的问题。
NP 完全性及其性质
- 设 $L$ 是任意一个 NPC 问题。
定理
- 如果 $L$ 存在一个多项式时间算法,那么对于每个 $L’ \in \mathcal{N}\mathcal{P}$,也存在一个多项式时间算法。
- 如果 $L$ 不存在多项式时间算法,那么对于任意 $L’ \in \mathcal{N}\mathcal{P}\mathcal{C}$,也不存在多项式时间算法。
证明
- 根据 NPC 的定义,对于每个 $L’ \in \mathcal{N}\mathcal{P}$,有 $L’ \leq_P L$。由于 $L \in \mathcal{P}$,根据第 6 页的定理,$L’ \in \mathcal{P}$。
- 根据上述结论。
$P \subseteq NP$, $NPC \subseteq NP$
$P = NP$ 吗?
开放性问题!可能非常困难。
通常认为 $P \neq NP$。
- 从 NP 完全问题的定义来看,证明一个问题 $L \in NPC$ 似乎是不可能的!
- 根据定义,这需要我们证明对于每一个 $L’ \in NP$,都有 $L’ \leq_P L$。
- 但是,NP 中有无限多个问题,我们如何证明从每个 $L’$ 到 $L$ 的归约都存在呢?
- 幸运的是,由于归约关系 $\leq_P$ 的 传递性 属性,我们有一种替代方法来证明决策问题 $L \in NPC$:
- (a) $L \in NP$;
- (b) 对某个 $L’ \in NPC$,有 $L’ \leq_P L$。
证明 设 $L’’$ 是任意一个 $NP$ 中的问题。由于 $L’$ 是 NP 完全问题,有 $L’’ \leq_P L’$。又因为 $L’ \leq_P L$,根据传递性,$L’’ \leq_P L$。
NPC 问题例子:找最大团(最大完全子图)、找独立集(一个点集,其中点之间两两没有边相连)
库克定理:$SAT \in NPC$
NP-hard:不一定是 NP 问题,但是所有 NP 问题可以在多项式时间内规约到它(可以视作是NPC问题的拓展)。例子:求最小顶点覆盖。
处理 hard problems
性能比(Performance Ratios)
- 设 $C$ 为近似算法返回的解的成本,$C^*$ 为最优解的成本。
算法在输入规模 $n$ 下的近似比 $\rho(n)$ 定义为:
\[\max\left(\frac{C}{C^*}, \frac{C^*}{C}\right) \leq \rho(n)\]- 近似比衡量近似解与最优解相比的劣化程度。
- 较大的近似比表示解比最优解差得多。
- 较小的近似比表示解与最优解相差无几。
最小顶点覆盖
顶点覆盖(Vertex-Cover):图 $G$ 的一个顶点覆盖是顶点的一个集合,使得图中每条边都至少与这些顶点中的一个相连。
最小顶点覆盖(Minimum Vertex Cover):找到给定图的最小大小顶点覆盖。我们称这样的顶点覆盖为最优顶点覆盖(optimal vertex cover),记为 $C^*$。
在二分图中,最大匹配(Maximum Matching)的大小等于最小顶点覆盖(Minimum Vertex Cover)的大小。
这种关系是König定理的一个经典结果,适用于二分图。
- 匹配(Matching):
- 在一个无向图 $G = (V, E)$ 中,若边的集合 $M \subseteq E$ 满足:每个顶点最多出现在 ( M ) 中的一条边上,则称 ( M ) 是一个匹配。
- 最大匹配(Maximum Matching):
- 给定一个图,找到一个匹配 ( M ),使得 ( M ) 的大小(即边的数量)最大。
最小集合覆盖
定义:
给定一个基础集合 UU(包含 nn 个元素)和一个子集的集合 S∗={S1,S2,…,Sk}S^* = {S_1, S_2, \ldots, S_k},每个子集 Si⊆US_i \subseteq U 有一个对应的成本 c(Si)c(S_i)。
目标:找到一个子集集合的子集
S∗⊆{S1,S2,…,Sk}S^* \subseteq {S_1, S_2, \ldots, S_k}
,使得:
- 这些子集覆盖了 UU 中的所有元素。
- S∗S^* 的总成本 ∑Si∈S∗c(Si)\sum_{S_i \in S^*} c(S_i) 最小。
顶点覆盖作为特殊情况:
- 图解释:
- 将集合覆盖问题中的元素 UU 视为黑色顶点。
- 将子集 S∗S^* 视为白色顶点,子集和元素之间有边相连(若元素属于某子集)。
- 顶点覆盖问题对应:
- 顶点覆盖问题等价于在图中选择一个最小集合的白色顶点,使得所有黑色顶点都被至少一条边覆盖。
- 因此,顶点覆盖问题可以被看作是集合覆盖问题的一个特例。
NP 问题判断题合集
任何 NP 完全问题都不存在多项式时间内的解法。
答案
无法判断正误。如果 P=NP,那么 NPC 就会有多项式时间内解法。P 类问题是 NP 类问题的真子集。
答案
无法判断正误。P=NP 尚未证明或证否。对某问题 $X \in NP$ 而言,若可以证明规约式 $3-SAT \leq_p X$,则 $X \in NPC$。
答案
正确对于一个 $NP$ 完全问题,其所有种类的输入均需要用指数级的时间求解。
答案
错误。NP 和 NPC 的定义考虑的是“最坏情况”下的复杂度,不意味着所有输入下复杂度都是指数级的。可能存在一些输入,多项式时间下就能求解。$NP\text{-}hard$ 类问题是 $NP$ 类问题的子集。
答案
错误。NP-hard 可以不是 NP。如果 $3\text{-}SAT \leq_p 2\text{-}SAT$,那么 $P = NP$。
答案
正确。NPC 可以归约到 P,则 NP 归约到 NPC 归约到 P,NP 可以在多项式时间复杂度内解决。$P$ 类问题是 $NP$ 类问题的真子集。
答案
无法判断。目前没有证据证明 P 是否等于 NP.若 $SAT$ 问题可以用复杂度为 $O(n^9)$ 的算法来解决,则所有的 $NP$ 完全问题都可以在多项式时间内被解决。
答案
正确。所有 NP 都可以规约到这个问题上。存在一个 $NP$ 完全问题可以在多项式时间内求解。
答案
无法判断。如果存在某一 $NP$ 问题不是多项式时间内可求解的,则所有 $NP$ 完全问题都不是多项式时间内可求解的。
答案
正确。说明该 NP 问题归约到 NPC 问题上后不是多项式时间内可解。判定无向图中是否存在环这一问题属于 $P$ 问题。
答案
正确。如果一个问题是 $NP\text{-}hard$,则一定存在一个算法可以在多项式时间内验证该问题的解。
答案
错误。NP-hard 可能不是 NP,则可能不能多项式时间内验证。如果假设 $P \neq NP$,则 $NP$ 完全问题可以在多项式时间内求解。
答案
错误。如果 NPC 可以在多项式时间复杂度内求解,则 P=NP,与假设矛盾。已知一个问题是 $NP$ 问题,如果该问题可以在多项式时间内求解,则可以证明 $P = NP$。
答案
错误。这个问题本身可能是 P 类问题。只有 NPC 问题被证明在多项式时间内可解,才可以得到 P=NP。给定一个包含 $n$ 个点的图 $G$,判断其中是否包含大小为 $10$ 的团不能在多项式时间内被解决。
答案
错误。这个问题可以通过枚举解决,复杂度是多项式时间。$UNSAT \in NP$($UNSAT$ 是指,给定一个布尔表达式 $\phi$,判断是否对其中变量的所有取值,$\phi$ 的值均为 $false$)。
答案
无法判断。这个问题可以给出一个“否”的证据,但是不能给出一个多项式时间内的证“正确”的证据(还是得枚举全部)。对某问题 $X \in NP$ 而言,若可以证明归约式 $X \leq_p 3\text{-}SAT$,则 $X$ 无法在多项式时间内被解决。
答案
错误。P 类问题属于 NP 问题,也可以归约到 3-SAT,但是可以在多项式时间内解决。